题目内容
若一个等差数列首项为0,公差为2,则这个等差数列的前20项之和为( )
| A、360 | B、370 |
| C、380 | D、390 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:根据等差数列的前n项和公式,求出结果即可.
解答:
解:根据等差数列的前n项和公式,得;
这个等差数列的前20项之和为
S20=20a1+
×20×19×d
=20×0+
×20×19×2
=380.
故选:C.
这个等差数列的前20项之和为
S20=20a1+
| 1 |
| 2 |
=20×0+
| 1 |
| 2 |
=380.
故选:C.
点评:本题考查了求等差数列的前n项和的应用问题,解题时应用公式直接计算,是基础题目.

练习册系列答案
相关题目
已知直线(a+2)x+y+8=0与直线(2a-1)x-(a+2)y-7=0垂直,则a=( )
A、-3±
| ||
| B、0或-2 | ||
| C、1或-2 | ||
D、
|
为了得到函数y=sin2x的图象,只需把函数y=cos2x的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
实数“a=1”是“直线l1:(a+1)x-y+1=0和l2:(2a-1)x+2y-1=0”垂直的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要 |
已知函数f(x)=
sin2x,则f(x+
)是( )
| 1 |
| 2 |
| 3π |
| 4 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
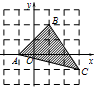 已知点A(-1,0),B(1,2),C(3,-1),点P(x,y)为△ABC边界及内部(如图阴影部分)的任意一点,则z=x-2y的最小值为
已知点A(-1,0),B(1,2),C(3,-1),点P(x,y)为△ABC边界及内部(如图阴影部分)的任意一点,则z=x-2y的最小值为