题目内容
不等式(x-1)(2-x)≥0的解集是( )
| A、{x|1≤x≤2} |
| B、{x|x≥1或x≤2} |
| C、{x|1<x<2} |
| D、{x|x>1或x<2} |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:把不等式(x-1)(2-x)≥0化为(x-1)(x-2)≤0,求出解集即可.
解答:
解:不等式(x-1)(2-x)≥0可化为
(x-1)(x-2)≤0;
解得1≤x≤2,
∴不等式的解集是{x|1≤x≤2}.
故选:A.
(x-1)(x-2)≤0;
解得1≤x≤2,
∴不等式的解集是{x|1≤x≤2}.
故选:A.
点评:本题考查了一元二次不等式的解法与应用问题,是容易题目.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
为了得到函数y=sin2x的图象,只需把函数y=cos2x的图象( )
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知函数f(x)=
sin2x,则f(x+
)是( )
| 1 |
| 2 |
| 3π |
| 4 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
若f(x)=ax2+bx(a,b为非零实数)存在一个虚数x1,使f(x)为实数-c,则b2-4ac与(2ax1+b)2的关系为( )
| A、不能比较大小 |
| B、b2-4ac>(2ax1+b)2 |
| C、b2-4ac<(2ax1+b)2 |
| D、b2-4ac=(2ax1+b)2 |
等差数列{an}中有两项an和ak满足an=
,ak=
(其中m,k∈N*,且m≠k),则该数列前mk项之和是( )
| 1 |
| k |
| 1 |
| m |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A(1,0,0),B(0,-1,1),
+λ
与
(O为坐标原点)的夹角为120°,则实数λ的值为( )
| OA |
| OB |
| OB |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|
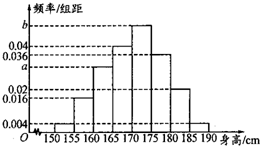 某校要调查高中二年级男生的身高情况,现从全年级男生中随机抽取一个容量为100的样本.样本数据统计如表,对应的频率分布直方图如图所示.
某校要调查高中二年级男生的身高情况,现从全年级男生中随机抽取一个容量为100的样本.样本数据统计如表,对应的频率分布直方图如图所示.