题目内容
已知点P(a,b)是椭圆
+y2=1上的一点,则b
的最大值为 .
| x2 |
| 4 |
| 1+a2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据点P是椭圆
+y2=1上的一点,利用基本不等式,求出b
的最大值.
| x2 |
| 4 |
| 1+a2 |
解答:
解:∵点P(a,b)是椭圆
+y2=1上的一点,
∴
+b2=1,
即a2+4b2=4;
∴b
=
≤
=
=
,
当且仅当2|b|=
,即b=±
时,“=”成立.
∴b
的最大值为
.
故答案为:
.
| x2 |
| 4 |
∴
| a2 |
| 4 |
即a2+4b2=4;
∴b
| 1+a2 |
2•2b•
| ||
| 4 |
| (2b)2+(1+a2) |
| 4 |
| 4b2+(1+a2) |
| 4 |
| 5 |
| 4 |
当且仅当2|b|=
| 1+a2 |
| ||
| 2 |
∴b
| 1+a2 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了椭圆的定义与几何性质的应用问题,也考查了基本不等式的应用问题,是综合题目.

练习册系列答案
相关题目
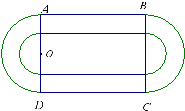 双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.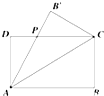 某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用,如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P,经试验当△ADP的面积最大时最节能.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用,如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P,经试验当△ADP的面积最大时最节能.