题目内容
已知函数f（x）是定义在R上的奇函数，在（0，2]上是增函数，且f（x-4）=-f（x），给出下列结论：
①若0＜x1＜x2＜4且x1+x2=4，则f（x1）+f（x2）＞0；
②若0＜x1＜x2＜4且x1+x2=5，则f（x1）＞f（x2）；
③若方程f（x）=m在[-8，8]内恰有四个不同的实根x1，x2，x3，x4，则x1+x2+x3+x4=-8或8；
④函数f（x）在[-8，8]内至少有5个零点，至多有13个零点
其中结论正确的有（ ）
①若0＜x1＜x2＜4且x1+x2=4，则f（x1）+f（x2）＞0；
②若0＜x1＜x2＜4且x1+x2=5，则f（x1）＞f（x2）；
③若方程f（x）=m在[-8，8]内恰有四个不同的实根x1，x2，x3，x4，则x1+x2+x3+x4=-8或8；
④函数f（x）在[-8，8]内至少有5个零点，至多有13个零点
其中结论正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：根的存在性及根的个数判断,奇偶性与单调性的综合
专题：函数的性质及应用
分析：先由“f（x）是奇函数且f（x-4）=-f（x）”转化得到f（x-8）=f（x），即函数f（x）为周期8的周期函数，然后按照条件↓
解答：
解：∵f（x）是奇函数且f（x-4）=-f（x），
∴f（x-8）=-f（x-4）=f（x），f（0）=0
∴函数f（x）为周期8的周期函数，根据题意可画出这样的图形：如图所示，
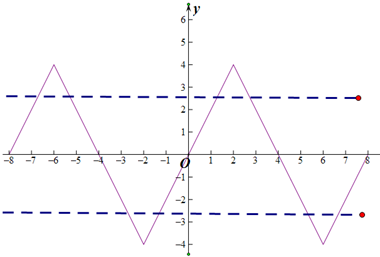
∵定义在R上的奇函数，在（0，2]上是增函数，
∴在（-2，0]上是增函数，
即（-2，2）上是增函数，
①若0＜x1＜x2＜4且x1+x2=4，则0＜x1＜2，2＜x2＜4，0＜4-x2＜2，-2＜x2-4＜0，
∴f（4-x2）＞f（x2-4），
又∵f（x1）=f（4-x2），-f（x2）=f（x2-4），
∴f（x1）＞-f（x2），即f（x1）+f（x2）＞0，故①正确；
②若0＜x1＜x2＜4且x1+x2=5，则0＜x1＜
，
＜x2＜5，观察可知f（x1）＞f（x2），故②正确；
③若方程f（x）=m在[-8，8]内恰有四个不同的实根x1，x2，x3，x4，当m＞0时（如上方虚线所示），可知
左边两个交点之和为-12（因为两个交点关于-6对称，一个交点可表示为-6-x0，另一个交点可表示为-6+x0），y轴右边的两个交点之和为4，则x1+x2+x3+x4=-8，同理m＜0时x1+x2+x3+x4=8，故③正确；
④函数f（x）在[-8，8]内有5个零点，故④不正确，
结论正确的有①②③，
故选：C
∴f（x-8）=-f（x-4）=f（x），f（0）=0
∴函数f（x）为周期8的周期函数，根据题意可画出这样的图形：如图所示，
∵定义在R上的奇函数，在（0，2]上是增函数，
∴在（-2，0]上是增函数，
即（-2，2）上是增函数，
①若0＜x1＜x2＜4且x1+x2=4，则0＜x1＜2，2＜x2＜4，0＜4-x2＜2，-2＜x2-4＜0，
∴f（4-x2）＞f（x2-4），
又∵f（x1）=f（4-x2），-f（x2）=f（x2-4），
∴f（x1）＞-f（x2），即f（x1）+f（x2）＞0，故①正确；
②若0＜x1＜x2＜4且x1+x2=5，则0＜x1＜
| 5 |
| 2 |
| 5 |
| 2 |
③若方程f（x）=m在[-8，8]内恰有四个不同的实根x1，x2，x3，x4，当m＞0时（如上方虚线所示），可知
左边两个交点之和为-12（因为两个交点关于-6对称，一个交点可表示为-6-x0，另一个交点可表示为-6+x0），y轴右边的两个交点之和为4，则x1+x2+x3+x4=-8，同理m＜0时x1+x2+x3+x4=8，故③正确；
④函数f（x）在[-8，8]内有5个零点，故④不正确，
结论正确的有①②③，
故选：C
点评：本题主要考查函数奇偶性周期性和单调性的综合运用，综合性较强题考查了函数的奇偶性，对称性及周期性的性质，解答此题的关键在于由已知等式得到函数对称轴方程和周期，属中档题
练习册系列答案
全程金卷系列答案
相关题目
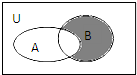设集合U={1，2，3，4，5}，A={2，3，4}，B={3，5}，则图中阴影部分所表示的集合为（ ）| A、{2，3} | B、{1，4} |
| C、{5} | D、{6} |
