题目内容
已知数列{an}的前n项和Sn=-an-(
)n+1+2(n为正整数).
(Ⅰ)令bn=2nan,求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=
an,Tn=c1+c2+…+cn,求Tn并证明:Tn<3.
| 1 |
| 2 |
(Ⅰ)令bn=2nan,求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=
| n+1 |
| n |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由Sn=-an-(
)n+1+2可求得2an=an-1+(
)n-1,结合bn=2nan,可证得bn=bn-1+1,从而可知其为等差数列,继而可求得数列{an}的通项公式;
(Ⅱ)由(I)得cn=
an=(n+1)(
)n,Tn=2×
+3×(
)2+4×(
)3+…+(n+1)×(
)n,
Tn=2×(
)2+3×(
)3+…+(n+1)×(
)n+1,利用错位相减法即可求得Tn=3-
,继而证得结论成立.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(I)得cn=
| n+1 |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n+3 |
| 2n |
解答:
(本小题满分14分)
证明:(Ⅰ)在Sn=-an-(
)n-1+2中,令n=1,可得S1=-an-1+2=a1,即a1=
…1分
当n≥2时,Sn-1=-an-1-(
)n-2+2,
∴an=Sn-Sn-1=-an+an-1+(
)n-1,
∴2an=an-1+(
)n-1…4分
即2nan=2n-1an-1+1…5分
∵bn=2nan,∴bn=bn-1+1,即当n≥2时,bn-bn-1=1…6分
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列…7分
于是bn=1+(n-1)•1=n=2nan,∴an=
…9分
(II)由(I)得cn=
an=(n+1)(
)n,
所以Tn=2×
+3×(
)2+4×(
)3+…+(n+1)×(
)n,
Tn=2×(
)2+3×(
)3+…+(n+1)×(
)n+1,….10分
由①-②得
Tn=1+(
)2+(
)3+…+(
)n-(n+1)×(
)n+1
=1+
-(n+1)×(
)n+1=
-
,
∴Tn=3-
,
∵
>0,所以Tn<3…14分
证明:(Ⅰ)在Sn=-an-(
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,Sn-1=-an-1-(
| 1 |
| 2 |
∴an=Sn-Sn-1=-an+an-1+(
| 1 |
| 2 |
∴2an=an-1+(
| 1 |
| 2 |
即2nan=2n-1an-1+1…5分
∵bn=2nan,∴bn=bn-1+1,即当n≥2时,bn-bn-1=1…6分
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列…7分
于是bn=1+(n-1)•1=n=2nan,∴an=
| n |
| 2n |
(II)由(I)得cn=
| n+1 |
| n |
| 1 |
| 2 |
所以Tn=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+
| ||||
1-
|
| 1 |
| 2 |
| 3 |
| 2 |
| n+3 |
| 2n+1 |
∴Tn=3-
| n+3 |
| 2n |
∵
| n+3 |
| 2n |
点评:本题考查数列的求和,考查等差关系的确定,突出考查错位相减法求数列的和,考查等价转化思想与综合运算、推理证明能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合A={x|y=
},集合B={y|y=x2,x∈R},则A∪B=( )
| x+1 |
| A、ϕ |
| B、[0,+∞) |
| C、[1,+∞) |
| D、[-1,+∞) |
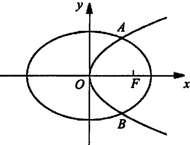 如图,已知椭圆C1:
如图,已知椭圆C1:
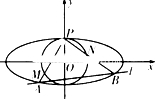 如图,椭圆C:
如图,椭圆C: