题目内容
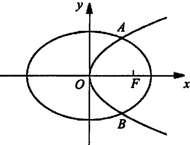 如图,已知椭圆C1:
如图,已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C1的方程;
(Ⅱ)求
| FA |
| FB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知条件得
,由此能求出椭圆C1方程.
(II)点A与点B关于x轴对称,设A(x0,y0)、B(x0,-y0),由点A在椭圆C1上,得y02=4(1-
),由已知有
=(x0-2,y0),
=(x0-2,-y0),由此能求出抛物线C2方程.
|
(II)点A与点B关于x轴对称,设A(x0,y0)、B(x0,-y0),由点A在椭圆C1上,得y02=4(1-
| x02 |
| 8 |
| FA |
| FB |
解答:
解:(I)∵椭圆C1:
+
=1(a>b>0)的离心率为
,右焦点为F(2,0),
∴
,解得a=2
,c=2…(3分)
由b2=a2-c2,得b=2…(4分)
故椭圆C1方程为
+
=1…(5分)
(II)点A与点B关于x轴对称,设A(x0,y0)、B(x0,-y0)…(6分)
由于点A在椭圆C1上,∴y02=4(1-
)
由已知有
=(x0-2,y0),
=(x0-2,-y0)…(7分)
则
•
=
-4x0+4-4(1-
)
=
-4x0=
(x0-
)2-
…(9分)
由于0-2
<x0<2
,
故当x0=
时,
•
取得最小值为-
…(10分)
当x0=
时,
=
,
又点A在抛物线C2上,代入抛物线C2方程得2p=
…(11分)
∴抛物线C2方程为y2=
x…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
| 2 |
由b2=a2-c2,得b=2…(4分)
故椭圆C1方程为
| x2 |
| 8 |
| y2 |
| 4 |
(II)点A与点B关于x轴对称,设A(x0,y0)、B(x0,-y0)…(6分)
由于点A在椭圆C1上,∴y02=4(1-
| x02 |
| 8 |
由已知有
| FA |
| FB |
则
| FA |
| FB |
| x | 2 0 |
| ||
| 8 |
=
| 3 |
| 2 |
| x | 2 0 |
| 3 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |
由于0-2
| 2 |
| 2 |
故当x0=
| 4 |
| 3 |
| FA |
| FB |
| 8 |
| 3 |
当x0=
| 4 |
| 3 |
| y | 2 0 |
| 28 |
| 9 |
又点A在抛物线C2上,代入抛物线C2方程得2p=
| 7 |
| 3 |
∴抛物线C2方程为y2=
| 7 |
| 3 |
点评:本题考查椭圆方程的求法,考查抛物线方程的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、对于函数y=f(x),若f(a)=0,则a是函数y=f(x)的零点 |
| B、方程f(x)=0有实数根,则函数y=f(x)有零点 |
| C、如果函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,且f(a)•f(b)<0,那么函数y=f(x)在区间[a,b]内至少有一个零点 |
| D、如果函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,且f(a)•f(b)>0,那么函数y=f(x)在区间[a,b]内一定有一个零点 |
y=x3在点M(-2,-8)处的切线方程是( )
| A、12x-y-16=0 |
| B、12x-y+16=0 |
| C、12x+y-16=0 |
| D、12x+y+16=0 |
已知命题“若p,则q”是真命题,对下列命题中一定是真命题的是( )
| A、若q,则p |
| B、¬p,则¬q |
| C、若¬q,则¬p |
| D、若¬p,则q |
函数函数f(x)=x2-4x+5-2lnx的零点个数为( )
| A、3 | B、2 | C、1 | D、0 |
 直三棱柱ABC-A1B1C1中,AB⊥AC,AC=AA1,AC1与A1C交于一点P,延长B1B到D,使得BD=
直三棱柱ABC-A1B1C1中,AB⊥AC,AC=AA1,AC1与A1C交于一点P,延长B1B到D,使得BD=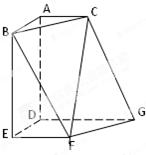 如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.
如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.