题目内容
求函数y=-2x+
+1的最大值和最小值．
| x |
考点：函数的最值及其几何意义
专题：
分析：先对原函数求导数，从而找出原函数的单调区间，然后根据单调性求最值即可．
解答：
解：y′=
-2，解
-2＞0得：0＜x＜
，所以原函数在（0，
]上是增函数，所以y≤
，x=0时，y=1，所以1≤y≤
；
解
-2＜0得：x＞
，所以原函数在[
，+∞）上是减函数，所以y≤
，所以原函数最大值是
，无最小值．
| 1 | ||
2
|
| 1 | ||
2
|
| 1 |
| 16 |
| 1 |
| 16 |
| 9 |
| 8 |
| 9 |
| 8 |
解
| 1 | ||
2
|
| 1 |
| 16 |
| 1 |
| 16 |
| 9 |
| 8 |
| 9 |
| 8 |
点评：一般让求函数最值的题目要先想到用函数单调性去求，要判断函数的单调性，求函数的单调区间，就要想到利用导数求解．
练习册系列答案
相关题目
已知x，y∈R，且命题p：x＞y，命题q：x-y+sin（x-y）＞0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数函数f（x）=x2-4x+5-2lnx的零点个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
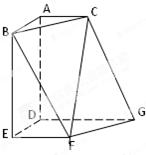如图，在多面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，BA⊥AC，ED⊥DG，EF∥DG且AC=1，AB=ED=EF=2，AD=DG=4．
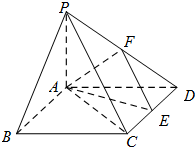如图在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=