题目内容
已知函数f(x)=ex-ax(a∈R),且函数f(x)的最小值为a.
(1)已知b∈R,设af(x)+bx>0,且{x|0≤x≤2}⊆P,求实数b的取值范围;
(2)设n∈N,证明
(
)n<
.
(1)已知b∈R,设af(x)+bx>0,且{x|0≤x≤2}⊆P,求实数b的取值范围;
(2)设n∈N,证明
 |
| k |
| n |
| e |
| e-1 |
考点:集合的包含关系判断及应用,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)先对函数f(x)进行求导,求出极值点为x=alna,根据函数f(x)的最小值为a,求出a=1,将题目转化成f(x)>-bx在[0,2]上恒成立,再利用导数求最值,问题得以解决.
(2)由(1)得,对于任意x∈R,都有ex-x≥1,即1+x≤ex,令x=-
(n∈N*,i=1,2,…,n-1),便可得到不等关系,将n项求和可得结论.
(2)由(1)得,对于任意x∈R,都有ex-x≥1,即1+x≤ex,令x=-
| 1 |
| n |
解答:
解:(1)∵f(x)=ex-ax(a∈R),
∴f′(x)=ex-a,
令f′(x)=ex-a=0,
解得x=lna,
即当x=lna时,函数f(x)有最小值.
∴f(lna)=a,
即a-alna=a,
解得a=1,a=0(舍去)
∵af(x)+bx>0,且{x|0≤x≤2}⊆P
∴ex-x+bx>0,
当x=0时,恒成立,
当0<x≤2时,
∴b>1-
恒成立
令g(x)=
,
则g′(x)=ex(
),
令g′(x)=ex(
)=0,
解得x=1,
即当x=1时,g(x)有最小值,最小值为g(1)=e,
∴b>1-e,
综上所述,实数b的取值范围是(1-e,+∞);
(2)证明:由(1)得,对于任意x∈R,都有ex-x≥1,即1+x≤ex.
令x=-
(n∈N*,i=1,2,…,n-1),则0<1-
<e-
∴(1-
)n<e-
=e-i(i=1,2,…,n-1),
即(
)n<e-i(i=1,2,…,n-1),
∴
(
)n=(
)n+(
)n+…+(
)n<e-(n-1)+e-(n-2)+…+e-1+1,
∵e-(n-1)+e-(n-2)+…+e-1+1=
<
=
,
∴
(
)n<
.
∴f′(x)=ex-a,
令f′(x)=ex-a=0,
解得x=lna,
即当x=lna时,函数f(x)有最小值.
∴f(lna)=a,
即a-alna=a,
解得a=1,a=0(舍去)
∵af(x)+bx>0,且{x|0≤x≤2}⊆P
∴ex-x+bx>0,
当x=0时,恒成立,
当0<x≤2时,
∴b>1-
| ex |
| x |
令g(x)=
| ex |
| x |
则g′(x)=ex(
| x-1 |
| x2 |
令g′(x)=ex(
| x-1 |
| x2 |
解得x=1,
即当x=1时,g(x)有最小值,最小值为g(1)=e,
∴b>1-e,
综上所述,实数b的取值范围是(1-e,+∞);
(2)证明:由(1)得,对于任意x∈R,都有ex-x≥1,即1+x≤ex.
令x=-
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
∴(1-
| 1 |
| n |
| 1 |
| n |
即(
| n-1 |
| n |
∴
| n |
 |
| k=1 |
| k |
| n |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
∵e-(n-1)+e-(n-2)+…+e-1+1=
| 1-e-n |
| 1-e-1 |
| 1 |
| 1-e-1 |
| e |
| e-1 |
∴
 |
| k |
| n |
| e |
| e-1 |
点评:本题考查了利用导数研究闭区间上的最值问题,恒成立问题的转化,以及不等式的证明.

练习册系列答案
相关题目
y=x3在点M(-2,-8)处的切线方程是( )
| A、12x-y-16=0 |
| B、12x-y+16=0 |
| C、12x+y-16=0 |
| D、12x+y+16=0 |
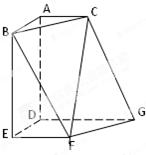 如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.
如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.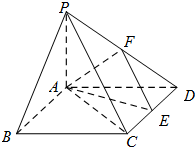 如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=
如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB= 某装修公司根据客户要求装饰一个墙角,施工设计时,在墙面交线AB与天花板ACD之间拉一条“定位线”EF(如图),已知墙面交线AB、AC、AD两两垂直,且AB=2,AC=AD=3.(单位:分米)
某装修公司根据客户要求装饰一个墙角,施工设计时,在墙面交线AB与天花板ACD之间拉一条“定位线”EF(如图),已知墙面交线AB、AC、AD两两垂直,且AB=2,AC=AD=3.(单位:分米)