题目内容
给出下列四个命题:
①函数y=sin(2x-
)的图象可由函数y=sin 2x的图象向右平移
个单位得到;
②函数y=lg x-sin 2x的零点个数为5;
③在锐角△ABC中,sin A+sin B+sin C>cos A+cos B+cos C;
④“等比数列{an}是递增数列”的一个充分不必要条件是“公比q>1”
其中所有正确命题的序号是 .
①函数y=sin(2x-
| π |
| 3 |
| π |
| 3 |
②函数y=lg x-sin 2x的零点个数为5;
③在锐角△ABC中,sin A+sin B+sin C>cos A+cos B+cos C;
④“等比数列{an}是递增数列”的一个充分不必要条件是“公比q>1”
其中所有正确命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,等差数列与等比数列,三角函数的图像与性质,简易逻辑
分析:根据三角函数的平移变换,函数零点概念以及结合图形的方法,锐角三角形中两锐角的和大于
,以及等比数列在公比q>1时的增减性即可判断每个命题的正误,从而找出正确命题的序号.
| π |
| 2 |
解答:
 解:①要由sin2x得到sin(2x-
解:①要由sin2x得到sin(2x-
)=sin2(x-
),应将sin2x的图象向右平移
个单位,∴①错误;
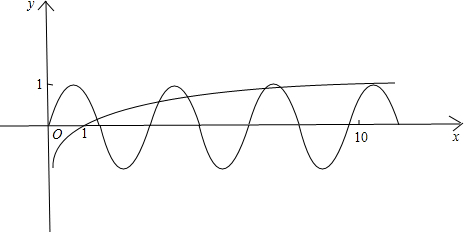
②令lgx-sin2x=0得lgx=sin2x,∴原函数零点个数便是函数lgx和函数sin2x交点个数,所以作lgx与sin2x图象如下:
lgx图象经过(1,0),(10,1),所以由图象可以看出在x=1和x=10之间有5个交点;
∴原函数有5个零点,所以②正确;
③∵△ABC是锐角三角形,所以:A+B>
,B+C>
,C+A>
;
∴A>
-B,且A,
-B∈(0,
);
所以sinA>sin(
-B),即sinA>cosB;
同理sinB>cosC,sinC>cosA;
∴sinA+sinB+sinC>cosA+cosB+cosC,即③正确;
④公比q>1不一定得到等比数列{an}是等比数列,比如等比数列:-1,-2,-22,-23,…;
该数列是首项为-1,公比为2的等比数列,显然是递减数列,所以④错误;
∴正确命题的序号是:②③.
故答案为:②③.
 解:①要由sin2x得到sin(2x-
解:①要由sin2x得到sin(2x-| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
②令lgx-sin2x=0得lgx=sin2x,∴原函数零点个数便是函数lgx和函数sin2x交点个数,所以作lgx与sin2x图象如下:
lgx图象经过(1,0),(10,1),所以由图象可以看出在x=1和x=10之间有5个交点;
∴原函数有5个零点,所以②正确;
③∵△ABC是锐角三角形,所以:A+B>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴A>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
所以sinA>sin(
| π |
| 2 |
同理sinB>cosC,sinC>cosA;
∴sinA+sinB+sinC>cosA+cosB+cosC,即③正确;
④公比q>1不一定得到等比数列{an}是等比数列,比如等比数列:-1,-2,-22,-23,…;
该数列是首项为-1,公比为2的等比数列,显然是递减数列,所以④错误;
∴正确命题的序号是:②③.
故答案为:②③.
点评:考查三角函数的平移变换:注意平移的单位数要看x的变化,函数零点的概念,以及通过图象求两函数图象交点个数的方法,以及在q>1时等比数列的增减性.

练习册系列答案
相关题目
 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn) (n∈N*)顺次为一次函数y=