题目内容
若幂函数f（x）的图象经过点（3，
），则其定义域为（ ）
| ||
| 3 |
| A、{x|x∈R，且x＞0} |
| B、{x|x∈R，且x＜0} |
| C、{x|x∈R，且x≠0} |
| D、R |
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：用待定系数法求出幂函数f（x）的解析式，再求f（x）的定义域．
解答：
解：设幂函数f（x）=xa，其图象过点（3，
），
∴3a=
；
解得a=-
，
∴f（x）=x-
=
；
∴x＞0，
即f（x）的定义域为{x|x∈R，且x＞0}．
故选：A．
| ||
| 3 |
∴3a=
| ||
| 3 |
解得a=-
| 1 |
| 2 |
∴f（x）=x-
| 1 |
| 2 |
| 1 | ||
|
∴x＞0，
即f（x）的定义域为{x|x∈R，且x＞0}．
故选：A．
点评：本题考查了幂函数的定义、图象与性质的应用问题，是基础题目．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
甲：函数f（x）是奇函数；乙：函数f（x）在定义域上是增函数．对于函数①f（x）=tanx，②f（x）=-
，③f（x）=x|x|，④f（x）=
能使甲、乙均为真命题的所有函数的序号是（ ）
| 1 |
| x |
|
| A、①② | B、②③ | C、③④ | D、②③④ |
下列函数为奇函数的是（ ）
| A、y=x2-1 | ||
| B、y=2x | ||
C、y=
| ||
D、y=
|
复数z满足|z|＜1，且|
+
|=
，则|z|=（ ）
. |
| z |
| 1 |
| z |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
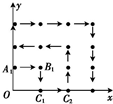为防洪抗旱，某地区大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在A1（0，1）点，第二棵树在B1（1，1）点，第三棵树在C1（1，0）点，第四棵树在C2（2，0）点，接着按图中箭头方向每隔一个单位长度种一棵树，那么，第2013棵树所在的点的坐标是