题目内容
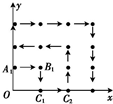为防洪抗旱，某地区大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在A1（0，1）点，第二棵树在B1（1，1）点，第三棵树在C1（1，0）点，第四棵树在C2（2，0）点，接着按图中箭头方向每隔一个单位长度种一棵树，那么，第2013棵树所在的点的坐标是考点：等差数列的通项公式
专题：等差数列与等比数列
分析：OA1B1C1设为第一个正方形，种植3棵树，第二个正方形种植5棵树，第三个正方形种植7棵树，…，构成等差数列，由等差数列的求和公式和通项公式可得．
解答：
解：∵OA1B1C1设为第一个正方形，种植3棵树，
依次下去，第二个正方形种植5棵树，第三个正方形种植7棵树，…，
可得树的棵树构成2为公差的等差数列，
前43个正方形共有43×3+
×2=1935棵树．
又2013-1935=78，78-44=34，45-34=11，
∴第2013棵树在（11，44）点处．
故答案为：（11，44）
依次下去，第二个正方形种植5棵树，第三个正方形种植7棵树，…，
可得树的棵树构成2为公差的等差数列，
前43个正方形共有43×3+
| 43×42 |
| 2 |
又2013-1935=78，78-44=34，45-34=11，
∴第2013棵树在（11，44）点处．
故答案为：（11，44）
点评：本题考查等差数列的通项公式，由题意找出规律是解决问题的关键，属基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
在平面直角坐标系中，以点C（-1，3）为圆心的圆与双曲线r：
-
=1（a＞0，b＞0）的一条渐近线相切，与另一条渐近线相交A，B两点，若劣弧
所对的圆心角为120°，则该双曲线的离心率e等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
 |
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若幂函数f（x）的图象经过点（3，
），则其定义域为（ ）
| ||
| 3 |
| A、{x|x∈R，且x＞0} |
| B、{x|x∈R，且x＜0} |
| C、{x|x∈R，且x≠0} |
| D、R |
设全集为R，函数f（x）=
的定义域为M，则M为（ ）
| x2-1 |
| A、（-∞，-1）∪（1，+∞） |
| B、[0，1） |
| C、（0，1] |
| D、（-∞，-1]∪[1，+∞） |