题目内容
1.已知二次函数f(x)=x2+ax+b的图象经过A(1,-4)、B(-1,0)两点.(1)关于x的方程f(x)=k有两个不相等的实根,求k的取值范围;
(2)求f(x)在区间[0,4]上的最大值及最小值.
分析 (1)由题意可得f(1)=-4,f(-1)=0,解方程可得a,b,进而得到函数的解析式,求得最小值,即可得到k的范围;
(2)求出对称轴,讨论区间和对称轴的关系,得到单调区间,即可得到最值.
解答 解:(1)由f(x)=x2+ax+b的图象经过A(1,-4)、B(-1,0)两点,
得$\left\{\begin{array}{l}{f(1)=1+a+b=-4}\\{f(-1)=1-a+b=0}\end{array}\right.$,解得a=-2,b=-3,
即有f(x)=x2-2x-3,当x=1时,f(x)取得最小值,且为-4,
由f(x)=k有两个相异的实根,可得k>-4.
故k的取值范围是(-4,+∞);
(2)由于二次函数的对称轴x=1,
可得f(x)在区间[0,1]上为减函数,在区间[1,4]上为增函数,
而f(1)=-4,f(4)=5,f(0)=-3,
故f(x)在区间[0,4]上的最小值为-4,最大值为5.
点评 本题考查二次函数的解析式的求法和函数方程的转化思想,考查二次函数在闭区间上的最值的求法,注意讨论对称轴和区间的关系,属于中档题.

练习册系列答案
相关题目
9.设全集U是实数集R,M={x|x2>4},N={x|1<x<3},则图中阴影部分所表示的集合是( )
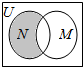

| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
13.直线x+2y-5=0与2x+4y+a=0之间的距离为$\sqrt{5}$,则a等于( )
| A. | 0 | B. | -20 | C. | 0或-20 | D. | 0或-10 |
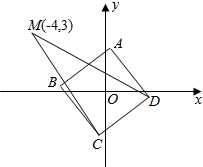 如图所示,ABCD是以原点O为中心、边长为2的正方形,M点坐标为(-4,3),当正方形在满足上述条件下转动时,$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15,35].
如图所示,ABCD是以原点O为中心、边长为2的正方形,M点坐标为(-4,3),当正方形在满足上述条件下转动时,$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15,35].