题目内容
16．
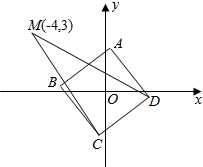如图所示，ABCD是以原点O为中心、边长为2的正方形，M点坐标为（-4，3），当正方形在满足上述条件下转动时，$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15，35]．
分析 由题意可设$\overrightarrow{OC}$+$\overrightarrow{OD}$、$\overrightarrow{MO}$的夹角为θ，则$\overrightarrow{MC}$•$\overrightarrow{MD}$=（$\overrightarrow{MO}$+$\overrightarrow{OC}$）•（$\overrightarrow{MO}$+$\overrightarrow{OD}$）=$\overrightarrow{MO}$2+（$\overrightarrow{OC}$+$\overrightarrow{OD}$）•$\overrightarrow{MO}$+$\overrightarrow{OC}$•$\overrightarrow{OD}$，再由$\overrightarrow{OC}$⊥$\overrightarrow{OD}$及$\overrightarrow{MO}$2=25，|$\overrightarrow{OC}$+$\overrightarrow{OD}$|=2，代入即可得到25+10cosθ，由余弦函数的值域，即可得到所求范围．
解答 解：记$\overrightarrow{OC}$+$\overrightarrow{OD}$、$\overrightarrow{MO}$的夹角为θ，
则$\overrightarrow{MC}$•$\overrightarrow{MD}$=（$\overrightarrow{MO}$+$\overrightarrow{OC}$）•（$\overrightarrow{MO}$+$\overrightarrow{OD}$）=$\overrightarrow{MO}$2+（$\overrightarrow{OC}$+$\overrightarrow{OD}$）•$\overrightarrow{MO}$+$\overrightarrow{OC}$•$\overrightarrow{OD}$，
由$\overrightarrow{OC}$⊥$\overrightarrow{OD}$及$\overrightarrow{MO}$2=25，|$\overrightarrow{OC}$+$\overrightarrow{OD}$|=2，
则$\overrightarrow{MC}$•$\overrightarrow{MD}$=25+|$\overrightarrow{OC}$+$\overrightarrow{OD}$|•|$\overrightarrow{MO}$|•cosθ=25+10cosθ，
由-1≤cosθ≤1，可得$\overrightarrow{MC}•\overrightarrow{MD}$的最小值为25-10=15；
最大值为25+10=35．
则$\overrightarrow{MC}•\overrightarrow{MD}$的取值范围是[15，35]．
故答案为：[15，35]．
点评 本题考查向量的数量积的定义和性质：向量的平方即为模的平方，同时考查余弦函数的值域，考查运算能力，属于中档题．
| A． | $\frac{2π}{3}$ | B． | $\frac{7π}{12}$ | C． | $\frac{7π}{6}$ | D． | $\frac{4π}{3}$ |
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | a＞c＞b |
| A． | $y=2sin（x+\frac{π}{6}）-2$ | B． | $y=2sin（x-\frac{π}{6}）+2$ | C． | $y=2sin（x-\frac{π}{6}）-2$ | D． | $y=2sin（x+\frac{π}{6}）+2$ |
| A． | 合情推理和演绎推理的结果都是正确的 | |
| B． | 若事件A，B是互斥事件，则A，B是对立事件 | |
| C． | 若事件A，B是对立事件，则A，B是互斥事件 | |
| D． | “复数z=a+bi（a，b∈R）是纯虚数”是“a=0”的必要不充分条件 |