题目内容
13．直线x+2y-5=0与2x+4y+a=0之间的距离为$\sqrt{5}$，则a等于（ ）| A． | 0 | B． | -20 | C． | 0或-20 | D． | 0或-10 |
分析 直线x+2y-5=0，可化为2x+4y-10=0，利用直线x+2y-5=0与2x+4y+a=0之间的距离为$\sqrt{5}$，建立方程，即可求出a．
解答 解：直线x+2y-5=0，可化为2x+4y-10=0，
∵直线x+2y-5=0与2x+4y+a=0之间的距离为$\sqrt{5}$，
∴$\frac{|a+10|}{\sqrt{4+16}}$=$\sqrt{5}$，
∴a=0或-20．
故选：C．
点评 本题考查两条平行线间的距离，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
18．如图，正方体ABCD-A1B1C1D1中，E为CC1中点，则下列结论中不正确的是（ ）
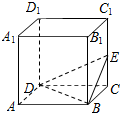
| A． | BD⊥A1C1 | B． | AC1∥平面BDE | ||
| C． | 平面BDE∥平面AB1D1 | D． | 平面A1BD⊥平面BDE |
5．下列说法正确的是（ ）
| A． | 合情推理和演绎推理的结果都是正确的 | |
| B． | 若事件A，B是互斥事件，则A，B是对立事件 | |
| C． | 若事件A，B是对立事件，则A，B是互斥事件 | |
| D． | “复数z=a+bi（a，b∈R）是纯虚数”是“a=0”的必要不充分条件 |