题目内容
已知函数y=lg
的定义域为集合A,集合B=(a,a+1),若B⊆A,求实数a的取值范围.
| 1+x |
| 1-x |
考点:对数函数的定义域
专题:函数的性质及应用,集合
分析:根据题意,求出函数y的定义域集合A,利用集合的运算,列出不等式组,求出a的取值范围.
解答:
解:∵函数y=lg
,
∴
>0,
等价于(1+x)(1-x)>0;
即(x+1)(x-1)<0,
解得-1<x<1;
∴函数y的定义域为集合A=(-1,1),
又∵集合B=(a,a+1),且B⊆A,
∴
,
解得-1≤a≤0;
∴a的取值范围是[-1,0].
| 1+x |
| 1-x |
∴
| 1+x |
| 1-x |
等价于(1+x)(1-x)>0;
即(x+1)(x-1)<0,
解得-1<x<1;
∴函数y的定义域为集合A=(-1,1),
又∵集合B=(a,a+1),且B⊆A,
∴
|
解得-1≤a≤0;
∴a的取值范围是[-1,0].
点评:本题考查了求对数函数的定义域的问题以及集合的简单运算问题,是基础题目.

练习册系列答案
相关题目
用更相减损术求30和18的最大公约数时,第三次作的减法为( )
| A、18-16=6 |
| B、12-6=6 |
| C、6-6=0 |
| D、30-18=12 |
在正方体ABCD-A1B1C1D1中向量表达式
-
+
化简后的结果是( )
| DD1 |
| AB |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
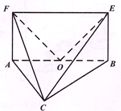 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.