题目内容
计算下列定积分,并从几何上解释这些值分别表示什么
(1)
x3dx;
(2)
x3dx;
(3)
x3dx.
(1)
| ∫ | 0 -1 |
(2)
| ∫ | 1 -1 |
(3)
| ∫ | 2 -1 |
考点:定积分
专题:导数的概念及应用
分析:利用导数的运算法则和微积分基本定理即可得出.
定积分
f(x)dx的几何意义是:若f(x)≥0,x∈[a,b],其几何意义是曲线y=f(x),x=a,x=b,y=0围成的曲边梯形的面积;
若f(x)≤0,x∈[a,b],其几何意义是曲线y=f(x),x=a,x=b,y=0围成的曲边梯形的面积的相反数;
若f(x)在区间[a,b]上有正有负时,其几何意义为曲线y=f(x)在x轴上方部分之下的曲边梯形的面积取正号,曲线y=f(x)在x轴下方部分之上的曲边梯形的面积取负号,构成的代数和.
定积分
| ∫ | b a |
若f(x)≤0,x∈[a,b],其几何意义是曲线y=f(x),x=a,x=b,y=0围成的曲边梯形的面积的相反数;
若f(x)在区间[a,b]上有正有负时,其几何意义为曲线y=f(x)在x轴上方部分之下的曲边梯形的面积取正号,曲线y=f(x)在x轴下方部分之上的曲边梯形的面积取负号,构成的代数和.
解答:
解:(1)∵(
x4)′=x3
∴
x3dx=(
x4)
=-
;
定积分
x3dx的几何意义指的是被积函数y=x3与直线x=-1,x=0,y=0所围成的图形的面积的相反数.
(2)∵(
x4)′=x3
∴
x3dx=(
x4)
=0;
定积分
x3dx的几何意义是曲线y=f(x)在x轴上方部分之下的曲边梯形的面积取正号,曲线y=f(x)在x轴下方部分之上的曲边梯形的面积取负号,构成的代数和.
(3)∵(
x4)′=x3
∴
x3dx=(
x4)
=
;
定积分
x3dx的几何意义是曲线y=f(x)在x轴上方部分之下的曲边梯形的面积取正号,曲线y=f(x)在x轴下方部分之上的曲边梯形的面积取负号,构成的代数和.
| 1 |
| 4 |
∴
| ∫ | 0 -1 |
| 1 |
| 4 |
| | | 0 -1 |
| 1 |
| 4 |
定积分
| ∫ | 0 -1 |
(2)∵(
| 1 |
| 4 |
∴
| ∫ | 1 -1 |
| 1 |
| 4 |
| | | 1 -1 |
定积分
| ∫ | 0 -1 |
(3)∵(
| 1 |
| 4 |
∴
| ∫ | 2 -1 |
| 1 |
| 4 |
| | | 2 -1 |
| 7 |
| 4 |
定积分
| ∫ | 2 -1 |
点评:本题主要考查定积分、定积分的几何意义,熟练掌握导数的运算法则和微积分基本定理是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

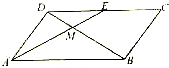 如图,在平行四边形ABCD中,E为DC的中点,AE与BD交于点E,AB=
如图,在平行四边形ABCD中,E为DC的中点,AE与BD交于点E,AB=