题目内容
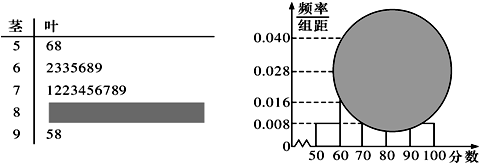
从某校高三数学学业水平测试卷中随机抽取部分试卷，对其成绩进行分析，因某特殊原因，所得的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图，则频率分布直方图中，从左往右第四个矩形的面积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：频率分布直方图
专题：图表型,概率与统计
分析：根据茎叶图求出数据在[50，60），[60，70），[70，80），[90，100）的频数，利用频数之比=矩形的高之比，求出第二，第三个小矩形的高，由频率分布直方图得第四个矩形的高，再乘以组距可得答案．
解答：
解：由茎叶图知数据在[50，60），[60，70），[70，80），[90，100）的频数分别为2、7，10，2，
∵频率分布直方图的小矩形的高之比=频数之比，
∴第二个矩形的高为7×
=0.028
∴第三个矩形的高为10×
=0.040，
∴频率分布直方图的第四个小矩形的高为0.016，
∴第四个矩形的面积为0.016×10=0.16=
．
故选B．
∵频率分布直方图的小矩形的高之比=频数之比，
∴第二个矩形的高为7×
| 0.008 |
| 2 |
∴第三个矩形的高为10×
| 0.008 |
| 2 |
∴频率分布直方图的第四个小矩形的高为0.016，
∴第四个矩形的面积为0.016×10=0.16=
| 4 |
| 25 |
故选B．
点评：本题考查了频率分布直方图与茎叶图，读懂图表中数据的含义是解答本题的关键，频率分布直方图小矩形的高=
| 频数 |
| 组距 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
双曲线C：
-
=1（a＞0，b＞0）的右焦点为F（c，0），以原点为圆心，c为半径的圆与双曲线在第二象限的交点为A，若此圆在A点处切线的斜率为
，则双曲线C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、
|
对任意两个非零的平面向量
和
，定义
o
=
，若平面向量
、
满足|
|＞|
|＞0，
与
夹角θ∈（0，
），且
o
和
o
都在集合{
|n∈Z}中，则
o
的取值个数最多为（ ）
| α |
| β |
| α |
| β |
| ||||
|
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 4 |
| a |
| b |
| b |
| a |
| n |
| 3 |
| a |
| b |
| A、2 | B、4 | C、6 | D、8 |
函数f（x）=
，满足对任意定义域中的x1，x2（x1≠x2），[f（x1）-f（x2）]（x1-x2）＜0总成立，则实数a的取值范围是（ ）
|
| A、（-∞，0） |
| B、[-1，0） |
| C、（-1，0） |
| D、（-1，+∞）， |
已知幂函数y=x
（|p|、|q|是互质的整数）的图象如图所示，则p、q的关系为（ ）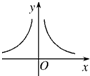
| p |
| q |
| A、pq＞0，p、q均为奇数 |
| B、pq＜0，p、q均为奇数 |
| C、pq＜0，p为奇数，q为偶数 |
| D、pq＜0，p为偶数，q为奇数 |
若x=
是f（x）=
sinωx+cosωx的图象的一条对称轴，则ω可以是（ ）
| π |
| 6 |
| 3 |
| A、4 | B、8 | C、2 | D、1 |
已知函数f（x）=ax2+2ax+1（-2＜a＜0），若x1＜x2，且x1+x2=a，则（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）＜f（x2） |
| C、f（x1）=f（x2） |
| D、f（x1），f（x2）大小不确定 |
| E、所以f（x1）＞f（x2） |