题目内容
17.已知椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点,若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为(1,0).分析 设A(-2,0),B(2,0),P(x0,y0),由椭圆方程和直线的斜率公式,以及两直线垂直的条件,计算即可得到定点坐标.
解答 解:设A(-2,0),B(2,0),P(x0,y0),
则$\frac{{{x}_{0}}^{2}}{4}$+$\frac{{{y}_{0}}^{2}}{3}$=1,即有y02=3(1-$\frac{{{x}_{0}}^{2}}{4}$),
设PA,PB的斜率为k1,k2,
则k1•k2=$\frac{{y}_{0}}{{x}_{0}-2}$•$\frac{{y}_{0}}{{x}_{0}+2}$=$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-4}$=-$\frac{3}{4}$,
设PA:y=k1(x+2),
则M(4,6k1),
PB:y=k2(x-2),则N(4,2k2),
又kDM=-$\frac{6{k}_{1}}{3}$=-2k1,kDN=-$\frac{2}{3}$k2,kDM•kDN=-1,
设圆过定点F(m,0),则$\frac{6{k}_{1}}{4-m}$•$\frac{2{k}_{2}}{4-m}$=-1,
解得m=1或m=7(舍去),
故过点D,M,N三点的圆是以MN为直径的圆过F(1,0).
故答案为:(1,0).
点评 本题考查椭圆的方程和性质,主要考查离心率公式的运用,同时考查直线的斜率公式的运用,圆的直径所对的圆周角为直角,属于中档题.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4.一个几何体的三视图,则该几何体的体积为( )
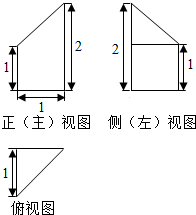

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
2.椭圆25x2+16y2=1的焦点坐标是( )
| A. | (±3,0) | B. | (±$\frac{1}{3}$,0) | C. | (±$\frac{3}{20}$,0) | D. | (0,±$\frac{3}{20}$) |
6.如图,在四形边ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使CD⊥平面ABD,构成三棱锥A-BCD.则在三棱锥A-BCD中,下列结论正确的是( )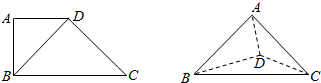

| A. | AD⊥平面BCD | B. | AB⊥平面BCD | C. | 平面BCD⊥平面ABC | D. | 平面ADC⊥平面ABC |
7.若a,b,c,d∈R,则“a+d=b+c”是“a,b,c,d依次成等差数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |