如图.在四形边ABCD中.AD∥BC.AD=AB.∠BCD=45°.∠BAD=90°．将△ADB沿BD折起.使CD⊥平面ABD.构成三棱锥A-BCD．则在三棱锥A-BCD中.下列结论正确的是( )A．AD⊥平面BCDB．AB⊥平面BCDC．平面BCD⊥平面ABCD．平面ADC⊥平面ABC 题目和参考答案——青夏教育精英家教网—

题目内容

6．如图，在四形边ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°．将△ADB沿BD折起，使CD⊥平面ABD，构成三棱锥A-BCD．则在三棱锥A-BCD中，下列结论正确的是（　　）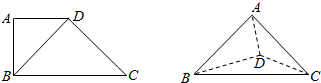

A．

AD⊥平面BCD

B．

AB⊥平面BCD

C．

平面BCD⊥平面ABC

D．

平面ADC⊥平面ABC

分析由题意推出CD⊥AB，AD⊥AB，推出AB⊥平面ADC，可得平面ABC⊥平面ADC．

解答解：∵在四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°
∴BD⊥CD
又平面ABD⊥平面BCD，且平面ABD∩平面BCD=BD
故CD⊥平面ABD，则CD⊥AB，又AD⊥AB
故AB⊥平面ADC，所以平面ABC⊥平面ADC．
故选D．

点评本题考查平面与平面垂直的判定，考查逻辑思维能力，是中档题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

17．已知椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$，A、B为椭圆C的左、右顶点，P为椭圆C上不同于A、B的动点，直线x=4与直线PA、PB分别交于M、N两点，若D（7，0），则过D、M、N三点的圆必过x轴上不同于点D的定点，其坐标为（1，0）．

14．已知椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1的弦AB的中点为M（3，2）．坐标原点为O．
（1）求直线AB的方程；
（2）求△AOB的面积．

1．

设P、Q是单位正方体AC₁的面AA₁D₁D、面A₁B₁C₁D₁的中心．
（1）求∠D₁B₁C的大小．
（2）证明：PQ∥平面AA₁B₁B．
（3）求异面直线PQ和B₁C所成的角．

11．直线l与抛物线y²=x交于A（x₁，y₁），B（x₂，y₂）两点，若y₁y₂=-4，则直线l过定点M，则点M的坐标为（1，0）．

18．设函数f（x）=（x-1）²-alnx，a∈R．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与直线x+2y-1=0垂直，求a的值；
（Ⅱ）求函数f（x）的单增区间．

15．下列幂函数在（-∞，0）上为减函数的是（　　）

A．

y=x${\;}^{\frac{1}{3}}$

16．甲、乙两人各自独立随机地从区间[0，1]任取一数，分别记为x、y，则x²+y²＞1的概率P=（　　）

试题分类