题目内容
已知函数f(x)=loga
(其中a>0且a≠1),g(x)是f(x+2)的反函数.
(1)已知关于x的方程loga
=f(x)在x∈[2,6]上有实数解,求实数m的取值范围;
(2)当0<a<1时,讨论函数f(x)的奇偶性和单调性;
(3)当0<a<1,x>0时,关于x的方程|g(x)|2+m|g(x)|+2m+3=0有三个不同的实数.
| x-1 |
| x+1 |
(1)已知关于x的方程loga
| m |
| (x+1)(7-x) |
(2)当0<a<1时,讨论函数f(x)的奇偶性和单调性;
(3)当0<a<1,x>0时,关于x的方程|g(x)|2+m|g(x)|+2m+3=0有三个不同的实数.
考点:对数函数的图像与性质
专题:计算题,作图题,函数的性质及应用
分析:(1)由题意,关于x的方程loga
=f(x)在x∈[2,6]上有实数解可转化为求函数m=(x-1)(7-x)在[2,6]上的值域,从而求解;
(2)先求定义域,再判断f(-x)=loga
=loga
=-f(x);利用单调性的定义求单调性;
(3)由g(x)的表达式,由表达式讨论g(x)的取值范围,从而求关于x的方程|g(x)|2+m|g(x)|+2m+3=0有三个不同的实数时m的取值范围.
| m |
| (x+1)(7-x) |
(2)先求定义域,再判断f(-x)=loga
| -x-1 |
| -x+1 |
| x+1 |
| x-1 |
(3)由g(x)的表达式,由表达式讨论g(x)的取值范围,从而求关于x的方程|g(x)|2+m|g(x)|+2m+3=0有三个不同的实数时m的取值范围.
解答:
 解:(1)由题意,关于x的方程loga
解:(1)由题意,关于x的方程loga
=f(x)在x∈[2,6]上有实数解可转化为
求函数m=(x-1)(7-x)在[2,6]上的值域,
该函数在[2,4]上递增、在[4,6]上递减,
则m的最小值5,最大值9,即m的取值范围为[5,9].
(2)f(x)=loga
的定义域为(-∞-1)∪(1,+∞),
定义域关于原点对称,
又∵f(-x)=loga
=loga
=-f(x),
∴所以函数f(x)为奇函数.
下面讨论在(1,+∞)上函数的增减性.
任取x1、x2∈(1,+∞),且x1<x2,令t(x)=
,
则t(x1)-t(x2)=
-
=
,
∵x1、x2∈(1,+∞),且x1<x2,
∴t(x1)-t(x2)<0.
又∵当0<a<1时,y=logax是减函数,
∴logat(x1)>logat(x2).
∴f(x)在(1,+∞)上函数是减函数.
又∵函数f(x)是奇函数,所以在(-∞-1)上函数也是减函数.
(3)f(x+2)的反函数是g(x)=
,
∵0<a<1,
∴g(x)=
=-3+
在(0,+∞)上单调递减,
又∵x>0,
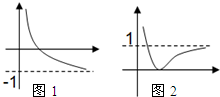
∴g(x)∈(-1,+∞),如图1.
令|g(x)|=t,(t≥0),如图2,
则方程t2+mt+2m+3=0的解应满足:
0<t1<1≤t2或
,
即
或m=-
(舍),
∴m∈(-
,-
].
 解:(1)由题意,关于x的方程loga
解:(1)由题意,关于x的方程loga| m |
| (x+1)(7-x) |
求函数m=(x-1)(7-x)在[2,6]上的值域,
该函数在[2,4]上递增、在[4,6]上递减,
则m的最小值5,最大值9,即m的取值范围为[5,9].
(2)f(x)=loga
| x-1 |
| x+1 |
定义域关于原点对称,
又∵f(-x)=loga
| -x-1 |
| -x+1 |
| x+1 |
| x-1 |
∴所以函数f(x)为奇函数.
下面讨论在(1,+∞)上函数的增减性.
任取x1、x2∈(1,+∞),且x1<x2,令t(x)=
| x-1 |
| x+1 |
则t(x1)-t(x2)=
| x1-1 |
| x1+1 |
| x2-1 |
| x2+1 |
| 2(x1-x2) |
| (x1+1)(x2+1) |
∵x1、x2∈(1,+∞),且x1<x2,
∴t(x1)-t(x2)<0.
又∵当0<a<1时,y=logax是减函数,
∴logat(x1)>logat(x2).
∴f(x)在(1,+∞)上函数是减函数.
又∵函数f(x)是奇函数,所以在(-∞-1)上函数也是减函数.
(3)f(x+2)的反函数是g(x)=
| 3ax-1 |
| 1-ax |
∵0<a<1,
∴g(x)=
| 3ax-1 |
| 1-ax |
| 2 |
| 1-ax |
又∵x>0,
∴g(x)∈(-1,+∞),如图1.
令|g(x)|=t,(t≥0),如图2,
则方程t2+mt+2m+3=0的解应满足:
0<t1<1≤t2或
|
即
|
| 3 |
| 2 |
∴m∈(-
| 3 |
| 2 |
| 4 |
| 3 |
点评:本题考查了函数的定义域,值域及单调性、奇偶性的判断与求法,同时考查了存在性命题的处理方法,属于难题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知函数f(x)=(
)x-lnx,若x0是函数f(x)的零点,且0<x1<x0,则f(x1)的值( )
| 1 |
| 6 |
| A、恒为正数 | B、等于0 |
| C、恒为负数 | D、不能确定正负 |
 已知函数f(x)=lg|x|.
已知函数f(x)=lg|x|.