Question

已知函数f（x）=lg|x|．
（1）判断函数f（x）的奇偶性；
（2）在如图直角坐标系中画出函数f（x）的草图；
（3）求函数f（x）的单调递减区间，并加以证明．

Answer 1

考点：函数图象的作法,函数单调性的判断与证明,函数奇偶性的判断

专题：函数的性质及应用

分析：（1）对于函数f（x）=lg|x|，根据它的定义域关于原点对称，f（-x）=f（x），可得函数为偶函数．
（2）先作出函数在（0，+∞）上的图象，再把所得图象关于y轴对称，即得函数在定义域上的图象．
（3）根据函数f（x）的图象，数形结合可得，函数的减区间．

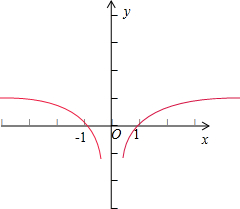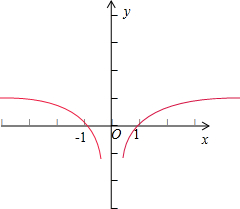解答： 解：（1）对于函数f（x）=lg|x|，它的定义域为{x|x≠0}，关于原点对称，
再根据f（-x）=lg|-x|=lg|x|=f（x），可得函数为偶函数．
（2）先作出函数在（0，+∞）上的图象，再把所得图象关于y轴对称，即得函数在定义域上的图象．
（3）数形结合可得，函数的减区间为（-∞，0）．

点评：本题主要考查函数的奇偶性的判断，函数的单调性，函数的图象的作法，属于基础题．