题目内容
设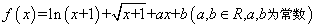 ,曲线
,曲线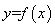 与直线
与直线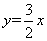 在
在 点相切.
点相切.
(1)求 的值;
的值;
(2)证明:当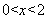 时,
时,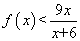
【解析】(1)由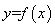 的图像过
的图像过 点,代入得
点,代入得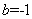
由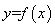 在
在 处的切线斜率为
处的切线斜率为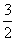 ,又
,又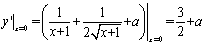 ,得
,得 …3分
…3分
(2)(证法一)由均值不等式,当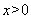 时,
时,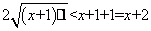 ,故
,故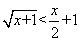
记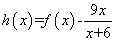 ,则
,则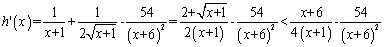
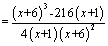 ,令
,令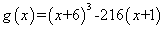 ,则当
,则当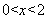 时,
时,
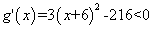
因此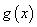 在
在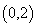 内是减函数,又由
内是减函数,又由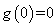 ,得
,得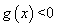 ,所以
,所以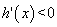
因此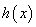 在
在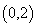 内是减函数,又由
内是减函数,又由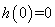 ,得
,得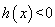 ,
,
于是当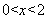 时,
时, 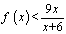 …12分
…12分
(证法二)
由(1)知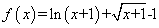 ,由均值不等式,当
,由均值不等式,当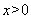 时,
时,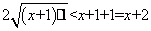 ,故
,故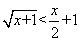
令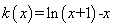 ,则
,则 ,故
,故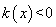 ,即
,即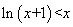 ,由此得,当
,由此得,当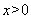 时,
时,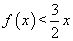 ,记
,记 ,则当
,则当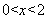 时,
时,
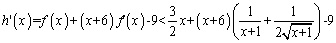
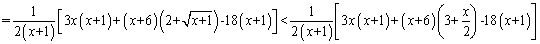
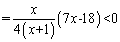
因此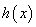 在
在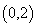 内是减函数,又由
内是减函数,又由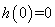 ,得
,得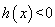 ,即
,即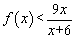

练习册系列答案
相关题目
 极大值为 .
极大值为 . 的实数根
的实数根 叫做函数
叫做函数 的“新驻点”,若函数
的“新驻点”,若函数 ,
, ,
, 的“新驻点”分别为
的“新驻点”分别为 ,则
,则 B.
B. C.
C. D.
D.
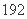 种 B.
种 B. 种 C.
种 C.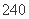 种 D.
种 D.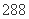 种
种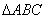 中,角
中,角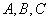 的对边分别为
的对边分别为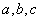 ,且
,且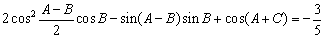 .
.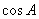 的值;
的值;
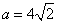 ,
,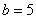 ,求向量
,求向量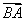 在
在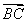 方向上的投影.
方向上的投影.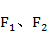 ,点A在C上.若|
,点A在C上.若|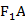 |=2|
|=2| |,则cos∠
|,则cos∠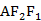 =( )
=( ) B.
B. C.
C.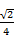 D.
D.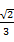
 的参数方程是
的参数方程是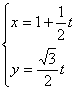 (
(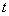 为参数),以原点
为参数),以原点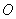 为极点,
为极点,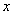 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆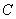 的极坐标方程为
的极坐标方程为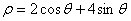 ,则直线
,则直线 B.81
B.81