题目内容
已知双曲线C的离心率为2,焦点为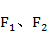 ,点A在C上.若|
,点A在C上.若|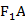 |=2|
|=2| |,则cos∠
|,则cos∠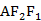 =( )
=( )
A. B.
B. C.
C.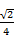 D.
D.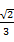
A

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
已知双曲线C的离心率为2,焦点为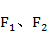 ,点A在C上.若|
,点A在C上.若|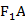 |=2|
|=2| |,则cos∠
|,则cos∠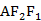 =( )
=( )
A. B.
B. C.
C.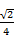 D.
D.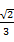
A

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案