题目内容
10.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=2+2t}\\{y=1-t}\end{array}\right.$(t为参数),椭圆C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),试在椭圆C上求一点P,使得点P到直线l的距离最小.分析 首先,根据直线l的参数方程为$\left\{\begin{array}{l}{x=2+2t}\\{y=1-t}\end{array}\right.$(t为参数),化简为普通方程为:x+2y=4,然后,设P(2cosθ,sinθ),根据点到直线的距离求解即可.
解答 解:根据直线l的参数方程为$\left\{\begin{array}{l}{x=2+2t}\\{y=1-t}\end{array}\right.$(t为参数),得其普通方程为:x+2y=4,
设P(2cosθ,sinθ),
∴P到l的距离为d=$\frac{|2cosθ+2sinθ-4|}{\sqrt{5}}$=$\frac{|2\sqrt{2}sin(θ+\frac{π}{4})-4|}{\sqrt{5}}$≥$\frac{4-2\sqrt{2}}{\sqrt{5}}$,
当且仅当sin(θ+$\frac{π}{4}$)=1,即θ=2kπ+$\frac{π}{4}$时等号成立.
此时,sinθ=cosθ=$\frac{\sqrt{2}}{2}$,
∴P($\sqrt{2}$,$\frac{\sqrt{2}}{2}$).
点评 本题重点考查了参数方程和普通的互化、点到直线的距离公式等知识,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
1.对于任意的实数a,b,c,下列命题正确的是( )
| A. | 若a>b,c=0,则ac>bc | B. | 若ac2>bc2,则a>b | ||
| C. | 若a>b,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a>b,则ac2>bc2 | ||
| E. | 若a>b,则ac2>bc2 |
19.已知向量$\overrightarrow a$=(-1,-2),$\overrightarrow b$=(1,λ),若$\overrightarrow a$,$\overrightarrow b$的夹角为钝角,则λ的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,2)∪(2,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | (2,+∞) |
20.已知定义在[-1,+∞]上的函数在区间[-1,3)上的解析式为f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}(-1≤x<1)}\\{\frac{3}{2}-\frac{3}{x}×|x-2|(1≤x<3)}\end{array}\right.$,当x≥3时,函数满足f(x)=f(x-4)+1,若函数g(x)=f(x)-kx-k有6个零点,则实数k的取值或取值范围为( )
| A. | ($\frac{5}{14}$,$\frac{9+\sqrt{21}}{40}$) | B. | $\frac{5}{14}$ | C. | ($\frac{5}{12}$,$\frac{1}{2}$) | D. | ($\frac{5}{14}$,$\frac{5}{12}$) |
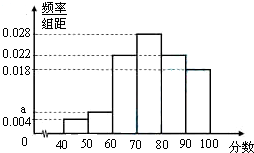 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]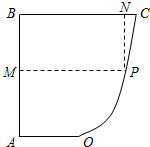 如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.
如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.