题目内容
15.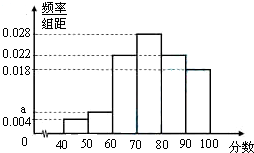 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100]
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100](1)求频率分布直方图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60)的受访职工中,随机抽取2人,求此2人的评分恰好有一人在[40,50)的概率.
分析 (1)利用频率分布直方图中的信息,所有矩形的面积和为1,得到a;
(2)对该部门评分不低于80的即为90和100,的求出频率,估计概率;
(3)求出评分在[40,60]的受访职工和评分都在[40,50]的人数,随机抽取2人,列举法求出所有可能,利用古典概型公式解答.
解答 解:(1)因为(0.004+a+0.018+0.022×2+0.028)×10=1,
解得a=0.006;
(2)由已知的频率分布直方图可知,
50名受访职工评分不低于80的频率为(0.022+0.018)×10=0.4,
所以该企业职工对该部门评分不低于80的概率的估计值为0.4;
(3)受访职工中评分在[50,60)的有:
50×0.006×10=3(人),记为A1,A2,A3;
受访职工评分在[40,50)的有:
50×0.004×10=2(人),记为B1,B2.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,
分别是{A1,A2},{A1,A3},{A1,B1},{A1,B2},
{A2,A3},{A2,B1},{A2,B2},{A3,B1},
{A3,B2},{B1,B2},
又因为所抽取2人的评分恰好有一人在[40,50)的结果有3种,
故所求的概率为:$p=\frac{6}{10}$=$\frac{3}{5}$.
点评 本题考查了频率分布直方图的认识以及利用图中信息求参数以及由频率估计概率,考查了利用列举法求满足条件的事件,并求概率.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
3.在单位圆中,一条弦AB的长度为$\sqrt{3}$,则该弦AB所对的弧长l为( )
| A. | $\frac{2}{3}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{6}$π | D. | π |
20.一元二次不等式-x2+4x+5<0的解集为( )
| A. | (-1,5) | B. | (-5,1) | C. | (-∞,-1)∪(5,+∞) | D. | (-∞,-5)∪(1,+∞) |
5.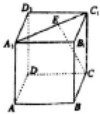 如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
 如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )
如图,在正方体ABCD-A1B1C1D1,若点E为A1C1上的一动点,则直线CE一定垂直于( )| A. | AC | B. | BD | C. | A1D | D. | A1D1 |