题目内容
5.已知函数f(x)满足f(x)=f(x+1)-f(x-1)(x∈R),且f(2)=1,则f(2012)=1.分析 由题设条件知,可构造出f(x+1)=f(x)+f(x+2),与f(x)=f(x-1)+f(x+1)联立解出函数的周期,再求函数值.
解答 解:因为f(x)=f(x+1)-f(x-1)
所以f(x+1)=f(x+2)-f(x)即f(x+2)=-f(x+1)+f(x)
两式相加得f(x+2)=-f(x-1)
即:f(x+3)=-f(x)
∴f(x+6)=-f(x+3)=f(x)
f(x)是以6为周期的周期函数.
f(2)=1,2012=6×335+2,
∴f(2012)=f(2)=1.
故答案为:1.
点评 本题考查对抽象函数表达式的理解和运用,解题的关键是由恒等变形得出函数的周期,本题的难点观察出解题的方向是研究函数的周期性,此类题有一个明显的特征那就是题设条件中必有恒等式,且要求的函数值自变量与已知函数值的自变量差值较大,不可能通过恒等式变形求出,题后注意总结这一特征,方便以后遇到同类题时能快速想到解题的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.函数y=x2-2lnx的单调递减区间是( )
| A. | (-∞,-1]∪(0,1] | B. | [-1,0)∪(0,1] | C. | [1,+∞) | D. | (0,1] |
14.已知随机变量X~N(0,σ2),且P(X>2)=0.4,则P(-2≤X≤0)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.8 |
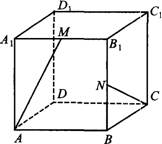 在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.