题目内容
20.设f(x)=$\frac{1}{{{4^x}+2}}$,利用课本中推导等差数列前n项和公式的方法,可求得f($\frac{1}{10}$)+f($\frac{2}{10}$)+…+f($\frac{9}{10}$)=$\frac{9}{4}$.分析 先考察函数f(x)具有的性质:若a+b=1,则f(a)+f(b)=$\frac{1}{2}$,由此可求答案.
解答 解:设a+b=1,则f(a)+f(b)=$\frac{1}{{4}^{a}+2}$+$\frac{1}{{4}^{b}+2}$=$\frac{1}{{4}^{a}+2}$+$\frac{1}{{4}^{1-a}+2}$
=$\frac{1}{{4}^{a}+2}$+$\frac{{4}^{a}}{4+2•{4}^{a}}$=$\frac{1}{2}$.
所以f($\frac{1}{10}$)+f($\frac{9}{10}$)=$\frac{1}{2}$,f($\frac{2}{10}$)+f($\frac{8}{10}$)=$\frac{1}{2}$,…,
∴f($\frac{1}{10}$)+f($\frac{2}{10}$)+…+f($\frac{9}{10}$)=$\frac{1}{2}$×(9×$\frac{1}{2}$)=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查根据数列是特殊的函数,根据函数具有的性质,来解决数列的和问题,利用的是倒序相加法,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
8.已知函数f(x)=4x2-1,若数列{${\frac{1}{f(n)$}前n项和为Sn,则S2018的值为( )
| A. | $\frac{2017}{2018}$ | B. | $\frac{2016}{2018}$ | C. | $\frac{4036}{4037}$ | D. | $\frac{2018}{4037}$ |
9.与y=|x|为同一函数的是( )
| A. | y=($\sqrt{x}$)2 | B. | y=a${\;}^{{{log}_a}x}}$ | C. | y=$\left\{\begin{array}{l}x,(x>0)\\-x,(x<0)\end{array}$ | D. | y=$\sqrt{x^2}$ |
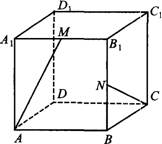 在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.
在正方体ABCD-A1B1C1D1中,M,N是棱A1B1,B1B的中点,求异面直线AM和CN所成角的余弦值.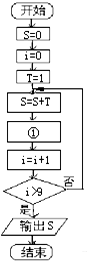 如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.
如图是在求:S=1+$\frac{1}{2}$+$\frac{1}{2^2}$+$\frac{1}{2^3}$+…+的一个程序框图.