题目内容
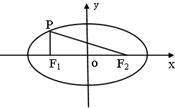 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
| 14 |
| 3 |
(1)求椭圆C的方程;
(2)若直线l过圆(x+2)2+(y-1)2=5的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由椭圆的定义,可得2a=6,a=3,再由勾股定理,即可得到c,再由a,b,c的关系,解得b,进而得到椭圆方程;
(2)设出直线l的方程,联立椭圆方程,消去y,得到x的方程,由中点坐标公式,即可得到k,检验判别式,即可得到直线方程.
(2)设出直线l的方程,联立椭圆方程,消去y,得到x的方程,由中点坐标公式,即可得到k,检验判别式,即可得到直线方程.
解答:
解:(1)由于|PF1|+|PF2|=2a=
+
=6,则a=3,
由PF1⊥F1F2,则|PF2|2-|PF1|2=|F1F2|2=(
)2-(
)2=20,
即有2c=2
,则c=
,b2=a2-c2=9-5=4,即b=2.
故椭圆C方程为:
+
=1;
(2)设A,B的坐标分别为(x1,y1),(x2,y2),
由圆的方程(x+2)2+(y-1)2=5,可知圆心M为(-2,1),
可设直线l的方程为:y=k(x+2)+1,代入椭圆C的方程,可得,
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0,
由于A,B关于点M对称,则
=-
=-2,解得k=
,
代入判别式△=(36k2+18k)2-4(4+9k2)(36k2+36k-27)>0,则成立.
所以直线l的方程为y=
(x+2)+1,即8x-9y+25=0.
| 4 |
| 3 |
| 14 |
| 3 |
由PF1⊥F1F2,则|PF2|2-|PF1|2=|F1F2|2=(
| 14 |
| 3 |
| 4 |
| 3 |
即有2c=2
| 5 |
| 5 |
故椭圆C方程为:
| x2 |
| 9 |
| y2 |
| 4 |
(2)设A,B的坐标分别为(x1,y1),(x2,y2),
由圆的方程(x+2)2+(y-1)2=5,可知圆心M为(-2,1),
可设直线l的方程为:y=k(x+2)+1,代入椭圆C的方程,可得,
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0,
由于A,B关于点M对称,则
| x1+x2 |
| 2 |
| 18k2+9k |
| 4+9k2 |
| 8 |
| 9 |
代入判别式△=(36k2+18k)2-4(4+9k2)(36k2+36k-27)>0,则成立.
所以直线l的方程为y=
| 8 |
| 9 |
点评:本题考查椭圆的定义吧、方程和性质,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理,以及中点坐标公式,注意不要忘记判别式的检验,属于中档题和易错题.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:其中正确命题的序号是( )
①若 m⊥α,n∥α,则m⊥n;
②若α∩γ=m,β∩γ=n,m∥n,则α∥β;
③若α∥β,β∥γ,m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β.
①若 m⊥α,n∥α,则m⊥n;
②若α∩γ=m,β∩γ=n,m∥n,则α∥β;
③若α∥β,β∥γ,m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β.
| A、①和③ | B、②和③ |
| C、③和④ | D、①和④ |