题目内容
已知f（x）=sin（ωx+
）（ω＞0），f（
）=f（
），且f（x）在区间（
，
）上有最大值无最小值，则ω= ．
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 12 |
| 5π |
| 6 |
考点：正弦函数的图象
专题：计算题,三角函数的图像与性质
分析：依题意，直线x=
=
为f（x）=sin（ωx+
）（ω＞0）的一条对称轴，且ω•
+
=2kπ+
（k∈Z），即可求得答案．
| ||||
| 2 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 2 |
解答：
解：∵f（x）=sin（ωx+
）（ω＞0），且f（
）=f（
），
在区间（
，
）上有最大值，无最小值，
∴直线x=
=
为f（x）=sin（ωx+
）（ω＞0）的一条对称轴，
∴ω•
+
=2kπ+
（k∈Z），
∴ω=4（2k+
）（k∈Z），又ω＞0，
∴当k=0时，ω=
．
故答案为：
．
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
在区间（
| π |
| 12 |
| 5π |
| 6 |
∴直线x=
| ||||
| 2 |
| π |
| 4 |
| π |
| 6 |
∴ω•
| π |
| 4 |
| π |
| 6 |
| π |
| 2 |
∴ω=4（2k+
| 1 |
| 3 |
∴当k=0时，ω=
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
点评：本题考查函数y=Asin（ωx+φ）的图象与性质，求得ω•
+
=kπ+
（k∈Z）是关键，也是难点，考查理解与运算能力，属于中档题．
| π |
| 4 |
| π |
| 6 |
| π |
| 2 |
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
已知M为椭圆
+
=1（a＞b＞0）上一点，F1、F2是两焦点，且∠MF1F2=2α，∠MF2F1=α，（α≠0），则椭圆的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、1-2sinα |
| B、2cosα-1 |
| C、1-cos2α |
| D、1-sin2α |
在正方形ABCD-A′B′C′D′中，棱长为1，求证：平面AB′C⊥平面BB′D′D．
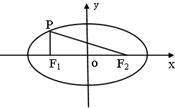椭圆C：