题目内容
设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：其中正确命题的序号是（ ）
①若 m⊥α，n∥α，则m⊥n；
②若α∩γ=m，β∩γ=n，m∥n，则α∥β；
③若α∥β，β∥γ，m⊥α，则m⊥γ；
④若α⊥γ，β⊥γ，则α∥β．
①若 m⊥α，n∥α，则m⊥n；
②若α∩γ=m，β∩γ=n，m∥n，则α∥β；
③若α∥β，β∥γ，m⊥α，则m⊥γ；
④若α⊥γ，β⊥γ，则α∥β．
| A、①和③ | B、②和③ |
| C、③和④ | D、①和④ |
考点：空间中直线与平面之间的位置关系
专题：证明题,空间位置关系与距离
分析：对于①，由线面平行的性质及线面垂直的定义可知正确；
对于②，α与β可能平行、相交；
对于③，由α∥β，β∥γ知α∥γ，由m⊥α知m⊥γ，故③正确；
对于④，α与β可能平行、相交．
对于②，α与β可能平行、相交；
对于③，由α∥β，β∥γ知α∥γ，由m⊥α知m⊥γ，故③正确；
对于④，α与β可能平行、相交．
解答：
解：对于①，由线面平行的性质及线面垂直的定义可知正确；
对于②，α与β可能平行、相交，故②错；
对于③，由α∥β，β∥γ知α∥γ，由m⊥α知m⊥γ，故③正确；
对于④，α与β可能平行、相交，故④错．
故选A．
对于②，α与β可能平行、相交，故②错；
对于③，由α∥β，β∥γ知α∥γ，由m⊥α知m⊥γ，故③正确；
对于④，α与β可能平行、相交，故④错．
故选A．
点评：本题考查空间中直线与平面之间的位置关系，考查学生分析解决问题的能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知M为椭圆
+
=1（a＞b＞0）上一点，F1、F2是两焦点，且∠MF1F2=2α，∠MF2F1=α，（α≠0），则椭圆的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、1-2sinα |
| B、2cosα-1 |
| C、1-cos2α |
| D、1-sin2α |
如图，在正方体A1B1C1D1-ABCD中，E，F分别为A1D与D1C的中点．
在正方形ABCD-A′B′C′D′中，棱长为1，求证：平面AB′C⊥平面BB′D′D．
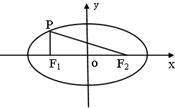椭圆C：