题目内容
在三棱锥V-ABC中,VB=6,AC=3,P为△VAC的重心,过点P作三棱锥的一个截面,使截面平行于直线VB和AC,则截面的周长为 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:如图所示,过点P作EF∥AC,分别交VA,VC于点E,F.过点F作FM∥VB交BC于点M,过点E作EN∥VB交AB于点N.由作图可知:四点EFMN共面.可得
=
=
,EF=MN=2.同理可得:EN=FM=2.
| EF |
| AC |
| MN |
| AC |
| 2 |
| 3 |
解答:
解:如图所示,过点P作EF∥AC,分别交VA,VC于点E,F.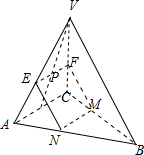
过点F作FM∥VB交BC于点M,过点E作EN∥VB交AB于点N.
由作图可知:EN∥FM,∴四点EFMN共面.
可得MN∥AC∥EF,EN∥VB∥FM.
∴
=
=
,
可得EF=MN=2.
同理可得:EN=FM=2.
∴截面的周长为8.
故答案为:8.

过点F作FM∥VB交BC于点M,过点E作EN∥VB交AB于点N.
由作图可知:EN∥FM,∴四点EFMN共面.
可得MN∥AC∥EF,EN∥VB∥FM.
∴
| EF |
| AC |
| MN |
| AC |
| 2 |
| 3 |
可得EF=MN=2.
同理可得:EN=FM=2.
∴截面的周长为8.
故答案为:8.
点评:本题考查了三角形重心的性质、线面平行的判定与性质定理、平行线分线段成比例定理,考查了推理能力用途计算能力,属于中档题.

练习册系列答案
相关题目
已知
≤k<1,函数f(x)=|2x-1|-k的零点分别为x1,x2(x1<x2),函数g(x)=|2x-1|-
的零点分别为x3,x4(x3<x4),则(x4-x3)+(x2-x1)的最小值为( )
| 1 |
| 5 |
| k |
| 2k+1 |
| A、log23 |
| B、2 |
| C、log26 |
| D、1 |
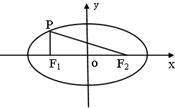 椭圆C:
椭圆C: