题目内容
17.某个容量为100的样本,频率分布直方图如图所示: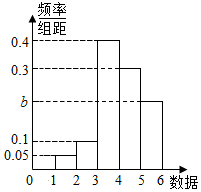
(1)求出b的值;
(2)根据频率分布直方图分别估计样本的众数与平均数.
分析 (1)根据频率和为1,列出方程求出b的值;
(2)根据频率分布直方图中最高的小矩形图底边的中点坐标得出样本的众数,再求出平均数.
解答 解:(1)根据频率和为1,得;
b=1-0.05-0.1-0.3-0.4=0.15;
(2)根据频率分布直方图中小矩形图最高的是3~4,
估计样本的众数是$\frac{3+4}{2}$=3.5;
平均数是1.5×0.05+2.5×0.1+3.5×0.4+4.5×0.3+5.5×0.15=3.9.
点评 本题考查了利用频率分布直方图求众数与平均数的应用问题,是基础题目.

练习册系列答案
相关题目
7.若{an}为等差数列,Sn是其前n项和,且S11=$\frac{22π}{3}$,{bn}为等比数列,b5•b7=$\frac{π^2}{4}$,则tan(a6+b6)的值为( )
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
6.在平面区域{(x,y)|0≤x≤1,1≤y≤2}内随机投入一点P,则点P的坐标(x,y)满足y≤2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |