题目内容
7.若{an}为等差数列,Sn是其前n项和,且S11=$\frac{22π}{3}$,{bn}为等比数列,b5•b7=$\frac{π^2}{4}$,则tan(a6+b6)的值为( )| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
分析 利用等差数列的和求出a6,等比数列的性质求出b6,然后求解即可.
解答 解:{an}为等差数列,Sn是其前n项和,且S11=$\frac{22π}{3}$,S11=11a6,∴a6=$\frac{2π}{3}$,
{bn}为等比数列,b5•b7=$\frac{π^2}{4}$,则b6=±$\frac{π}{2}$.
tan(a6+b6)=tan($\frac{2π}{3}$+$\frac{π}{2}$)=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$.
或tan(a6+b6)=tan($\frac{2π}{3}$-$\frac{π}{2}$)=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查数列求和,三角函数的化简求值,等差数列与等比数列的综合应用,考查计算能力.

练习册系列答案
相关题目
15.2016年1月6日北京时间上午11时30分,朝鲜中央电视台宣布“成功进行了氢弹试验”,再次震动世界,朝鲜声明氢弹试验对周边生态环境未产生任何负面影响,未提及试验地点.中国外交部发表措辞严厉的声明对朝鲜核试验“坚决反对”,朝鲜“氢弹试验”事件引起了我国公民热议,其中丹东市(丹东市和朝鲜隔江)某QQ聊天群有300名网友,新疆乌鲁木齐某微信群有200名微信好友,为了解不同地区我国公民对“氢弹试验”事件的关注程度,现采用分层抽样的方法,从中抽取了100名好友,先分别统计了他们在某时段发表的信息条数,再将两地网友留言信息条数分成5组:[40,50),[50,60),[60,70),[70,80),[80,90),分别加以统计,得到如图所示的频率分布直方图.
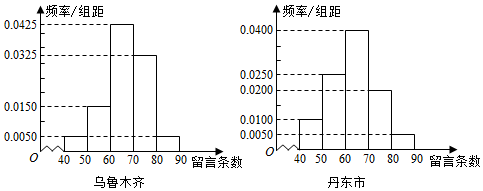
(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数不足50条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列2×2的列联表;
②判断是否有90%的把握认为“强烈关注”与网友所在的地区有关?
附:临界值表及参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.

(1)求丹东市网友的平均留言条数(保留整数);
(2)为了进一步开展调查,从样本中留言条数不足50条的网友中随机抽取2人,求至少抽到一名乌鲁木齐市网友的概率;
(3)规定“留言条数”不少于70条为“强烈关注”.
①请你根据已知条件完成下列2×2的列联表;
| 强烈关注 | 非强烈关注 | 合计 | |
| 丹东市 | 15 | 45 | 60 |
| 乌鲁木齐市 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
附:临界值表及参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12.已知集合A={x|x2-5x+6≤0},B={x∈Z|2x>1},则A∩B=( )
| A. | [2,3] | B. | (0,+∞) | C. | (0,2)∪(3,+∞) | D. | (0,2]∪[3,+∞) |
19.若函数f(x)=sin(2x+φ)(-π<φ<0)为偶函数,则函数f(x)在区间$[0,\frac{π}{4}]$上的取值范围是( )
| A. | [-1,0] | B. | $[-\frac{{\sqrt{2}}}{2},0]$ | C. | $[0,\frac{{\sqrt{2}}}{2}]$ | D. | [0,1] |