题目内容
9.在△ABC中,已知$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\sqrt{3}$,且∠BAC=30°,则△ABC的面积为1.分析 运用向量的数量积的定义,可得|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•cos30°=2$\sqrt{3}$,即有|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=4,再由三角形的面积公式计算即可得到所求值.
解答 解:由$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\sqrt{3}$,且∠BAC=30°,
可得|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•cos30°=2$\sqrt{3}$,
即有|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=4,
可得△ABC的面积为$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|sin30°=$\frac{1}{2}$•4•$\frac{1}{2}$=1.
故答案为:1.
点评 本题考查向量的数量积的定义,考查三角形的面积公式的运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若函数f(x)=sin(2x+φ)(-π<φ<0)为偶函数,则函数f(x)在区间$[0,\frac{π}{4}]$上的取值范围是( )
| A. | [-1,0] | B. | $[-\frac{{\sqrt{2}}}{2},0]$ | C. | $[0,\frac{{\sqrt{2}}}{2}]$ | D. | [0,1] |
20.设等差数列{an}的前n项和为Sn,且a2+a7+a12=24,则S13=( )
| A. | 52 | B. | 78 | C. | 104 | D. | 208 |
14.下列各组函数中,f(x)与g(x)表示同一函数的是( )
| A. | f(x)=x-1与g(x)=$\sqrt{{x}^{2}-2x+1}$ | B. | f(x)=x与g(x)=$\frac{{x}^{2}}{x}$ | ||
| C. | f(x)=x与g(x)=$\root{3}{x^3}$ | D. | f(x)=$\frac{{x}^{2}-4}{x-2}$与g(x)=x+2 |
1.不等式x2+x<$\frac{a}{b}$+$\frac{b}{a}$ 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| A. | (-2,0) | B. | (-∞,-2)∪(1,+∞) | C. | (-2,1) | D. | (-∞,-4)∪(2,+∞) |
18.化简$\sqrt{9{x^2}-6x+1}-{({\sqrt{3x-5}})^2}$,结果是( )
| A. | 6x-6 | B. | -6x+6 | C. | -4 | D. | 4 |
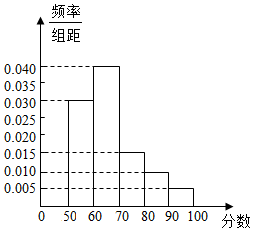 某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.