题目内容
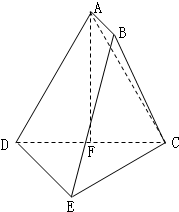 已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.(1)求证:AF⊥平面CDE;
(2)求平面ABC和平面CDE所成的锐二面角的大小.
考点:二面角的平面角及求法
专题:空间角
分析:(1)取CE的中点M,连接BM、FM,利用线面垂直的性质即可得到结论.
(2)以O为坐标原点,建立空间坐标系,求出各个顶点的坐标,进而求出平面ABC和BCE的法向量,利用向量法即可得到结论.
(2)以O为坐标原点,建立空间坐标系,求出各个顶点的坐标,进而求出平面ABC和BCE的法向量,利用向量法即可得到结论.
解答:
证明:(1)取CE的中点M,连接BM、FM,
∵F为CD的中点,
∴FM∥DE,且FM=
DE=
×2=1,
∵DE∥AB,
∴AB=1,
∴AB∥FM,且AB=FM,
则四边形ABMF为平行四边形,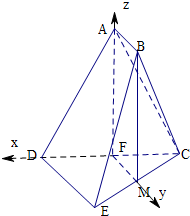
∵AB⊥平面ACD,AB∥FM
∴FM⊥平面ACD,
∴FM⊥AF,
∵AC=AD=CD=DE=2,
∴AF⊥CD,
又AF∩CD=F
∴AF⊥平面CDE.
解:( 2)以F为坐标原点,分别以FD、FM、FA为x轴、y轴、z轴建立空间坐标系,如图
则F(0,0,0),D(1,0,0),C(-1,0,0),A(0,0,
),B(0,1,
),
∵AF⊥平面CDE
∴
=(0,0,
)是平面BCE的一个法向量,
设
=(x,y,z)是平面ABC的一个法向量,
则
=(0,1,0),
=(1,0,
),
则
,
令z=1,则x=-
,y=0,
即
=(-
,0,1),
则平面ABC和平面CDE所成的锐二面角满足|cos<
,
>|=
=
=
,
则<
,
>=
,
即平面ABC和平面CDE所成的锐二面角的大小
.
∵F为CD的中点,
∴FM∥DE,且FM=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE∥AB,
∴AB=1,
∴AB∥FM,且AB=FM,
则四边形ABMF为平行四边形,

∵AB⊥平面ACD,AB∥FM
∴FM⊥平面ACD,
∴FM⊥AF,
∵AC=AD=CD=DE=2,
∴AF⊥CD,
又AF∩CD=F
∴AF⊥平面CDE.
解:( 2)以F为坐标原点,分别以FD、FM、FA为x轴、y轴、z轴建立空间坐标系,如图
则F(0,0,0),D(1,0,0),C(-1,0,0),A(0,0,
| 3 |
| 3 |
∵AF⊥平面CDE
∴
| FA |
| 3 |
设
| n |
则
| AB |
| CA |
| 3 |
则
|
令z=1,则x=-
| 3 |
即
| n |
| 3 |
则平面ABC和平面CDE所成的锐二面角满足|cos<
| FA |
| n |
|
| ||||
|
|
| ||||||
|
| 1 |
| 2 |
则<
| FA |
| n |
| π |
| 3 |
即平面ABC和平面CDE所成的锐二面角的大小
| π |
| 3 |
点评:本题考查的知识点是直线与平面垂直的性质及二面角的平面角及求法,在使用向量法求二面角的大小时,建立坐标系,求出平面的法向量是关键.

练习册系列答案
相关题目
设全集U=R,且A={x||x-1|>2},B={x|x2-6x+8<0},则(∁UA)∩B=( )
| A、[-1,4) |
| B、(2,3) |
| C、(2,3] |
| D、(-1,4) |
已知tanα=
,则
等于( )
| 1 |
| 2 |
| cos2α+sin2α+1 |
| cos2α |
| A、4 | ||
| B、6 | ||
| C、12 | ||
D、
|
已知数列{an}满足2an+1+an=0,a1=-2,则数列{an}的前10项和S10为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
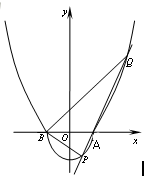 如图,由半椭圆x2+
如图,由半椭圆x2+