题目内容
设全集U=R，且A={x||x-1|＞2}，B={x|x2-6x+8＜0}，则（∁UA）∩B=（ ）
| A、[-1，4） |
| B、（2，3） |
| C、（2，3] |
| D、（-1，4） |
考点：绝对值不等式的解法,交、并、补集的混合运算,一元二次不等式的解法
专题：不等式的解法及应用
分析：利用绝对值是表达式的解法求出集合A，二次不等式的解法求解集合B，然后求解（∁UA）∩B．
解答：
解：A={x||x-1|＞2}={x|x＞3或x＜-1}，
∁UA={x|-1≤x≤3}．
B={x|x2-6x+8＜0}={x|2＜x＜4}，
∴（∁UA）∩B={x|2＜x≤3}．
故选：C．
∁UA={x|-1≤x≤3}．
B={x|x2-6x+8＜0}={x|2＜x＜4}，
∴（∁UA）∩B={x|2＜x≤3}．
故选：C．
点评：本题考查集合的基本运算，绝对值表达式以及二次不等式的解法，考查计算能力．
练习册系列答案
相关题目
一个扇形OAB的面积是1cm2，它的周长是4cm，则弦|AB|=（ ）
| A、sin1 | B、cos1 |
| C、2sin1 | D、sin2 |
设i是虚数单位，
（1+i）=3-i，则复数z=（ ）
| z |
| A、1-2i | B、1+2i |
| C、2-i | D、2+i |
不等式
＜
的解集是（ ）
| 1 |
| x |
| 1 |
| 2 |
| A、{x|x＜2} |
| B、{x|x＞2} |
| C、{x|0＜x＜2} |
| D、{x|x＜0或x＞2} |
已知抛物线y=ax2经过点（1，-
），则该抛物线的焦点坐标为（ ）
| 1 |
| 4 |
A、（0，-
| ||
B、（0，-
| ||
| C、（0，-1） | ||
| D、（0，1） |
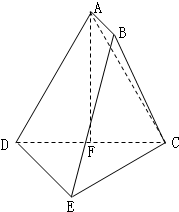已知在多面体ABCDE中，AB⊥平面ACD，AB=1，DE∥AB，AC=AD=CD=DE=2，F为CD的中点．