题目内容
已知数列{an}满足2an+1+an=0,a1=-2,则数列{an}的前10项和S10为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:由数列递推式得到数列为等比数列,然后由等比数列的前n项和得答案.
解答:
解:由2an+1+an=0,
得2an+1=-an,
∴
=-
,
又a1=-2,
∴S10=
=
(2-10-1).
故选:C.
得2an+1=-an,
∴
| an+1 |
| an |
| 1 |
| 2 |
又a1=-2,
∴S10=
-2[1-(-
| ||
1+
|
| 4 |
| 3 |
故选:C.
点评:本题考查了等比关系的确定,考查了等比数列的前n项和,是中档题.

练习册系列答案
相关题目
已知抛物线y=ax2经过点(1,-
),则该抛物线的焦点坐标为( )
| 1 |
| 4 |
A、(0,-
| ||
B、(0,-
| ||
| C、(0,-1) | ||
| D、(0,1) |
边长为5cm的正方形EFGH是圆柱的轴截面,则从E点沿圆柱的侧面到相对顶点G的最短距离是( )
| A、10 | ||||
B、
| ||||
C、5
| ||||
D、5
|
公比为2的等比数列{an} 中,a4a10+a3a11=32,则a6=( )
| A、1 | B、2 | C、±2 | D、4 |
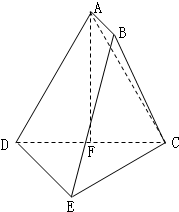 已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.