题目内容
袋中有3只红球,2只白球,1只黑球.
(1)若从袋中有放回的抽取3次,每次抽取一只,求恰有两次取到红球的概率.
(2)若从袋中有放回的抽取3次,每次抽取一只,求抽全三种颜色球的概率.
(3)若从袋中不放回的抽取3次,每次抽取一只.设取到1只红球得2分,取到1 只白球得1分,取到1只黑球得0分,试求得分ξ的数学期望.
(4)若从袋中不放回的抽取,每次抽取一只.当取到红球时停止抽取,否则继续抽取,求抽取次数η的分布列和数学期望.
(1)若从袋中有放回的抽取3次,每次抽取一只,求恰有两次取到红球的概率.
(2)若从袋中有放回的抽取3次,每次抽取一只,求抽全三种颜色球的概率.
(3)若从袋中不放回的抽取3次,每次抽取一只.设取到1只红球得2分,取到1 只白球得1分,取到1只黑球得0分,试求得分ξ的数学期望.
(4)若从袋中不放回的抽取,每次抽取一只.当取到红球时停止抽取,否则继续抽取,求抽取次数η的分布列和数学期望.
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:概率与统计
分析:(1)抽1次得到红球的概率为
,得白球的概率为
,得黑球的概率为
.由此能求出恰2次为红色球的概率.
(2)由抽1次得到红球的概率为
,得白球的概率为
,得黑球的概率为
,由此能求出抽全三种颜色球的概率.
(3)由已知得ξ=6,5,4,3,2,分别求出相应的概率,由此能求出求出得分ξ的数学期望.
(4)由已知得η=1,2,3,4,分别求出相应的概率,由此能求出求出抽取次数η的分布列和数学期望.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
(2)由抽1次得到红球的概率为
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
(3)由已知得ξ=6,5,4,3,2,分别求出相应的概率,由此能求出求出得分ξ的数学期望.
(4)由已知得η=1,2,3,4,分别求出相应的概率,由此能求出求出抽取次数η的分布列和数学期望.
解答:
解:(1)抽1次得到红球的概率为
,得白球的概率为
,得黑球的概率为
.
所以恰2次为红色球的概率为P1=
(
)2
=
…(2分)
(2)抽全三种颜色球的概率P2=(
×
×
)•
=
…(4分)
(3)ξ=6,5,4,3,2,
p(ξ=6)=
=
;
p(ξ=5)=
=
;
p(ξ=4)=
=
;
p(ξ=3)=
=
;
p(ξ=2)=
=
Eξ=6×
+5×
+4×
+3×
+2×
=4…(8分)
(4)η=1,2,3,4,
P(η=1)=
,
P(η=2)=
×
=
;
P(η=3)=
×
×
=
,
P(η=4)=
×
×
×
=
,
∴η的分布列是:
Eη=1×
+2×
+3×
+4×
=
…(12分)
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
所以恰2次为红色球的概率为P1=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
(2)抽全三种颜色球的概率P2=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| A | 3 3 |
| 1 |
| 6 |
(3)ξ=6,5,4,3,2,
p(ξ=6)=
| ||
|
| 1 |
| 20 |
p(ξ=5)=
| ||||
|
| 6 |
| 20 |
p(ξ=4)=
| ||||||||
|
| 6 |
| 20 |
p(ξ=3)=
| ||||||
|
| 6 |
| 20 |
p(ξ=2)=
| ||||
|
| 1 |
| 20 |
| 1 |
| 20 |
| 6 |
| 20 |
| 6 |
| 20 |
| 6 |
| 20 |
| 1 |
| 20 |
(4)η=1,2,3,4,
P(η=1)=
| 3 |
| 6 |
P(η=2)=
| 3 |
| 6 |
| 3 |
| 5 |
| 3 |
| 10 |
P(η=3)=
| 3 |
| 6 |
| 2 |
| 5 |
| 3 |
| 4 |
| 3 |
| 20 |
P(η=4)=
| 3 |
| 6 |
| 2 |
| 5 |
| 1 |
| 4 |
| 3 |
| 3 |
| 1 |
| 20 |
∴η的分布列是:
| η | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 6 |
| 20 |
| 3 |
| 20 |
| 1 |
| 20 |
| 7 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
公比为2的等比数列{an} 中,a4a10+a3a11=32,则a6=( )
| A、1 | B、2 | C、±2 | D、4 |
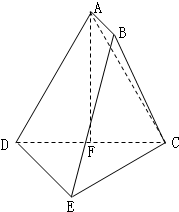 已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
已知在多面体ABCDE中,AB⊥平面ACD,AB=1,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.