题目内容
已知tanα=
，则
等于（ ）
| 1 |
| 2 |
| cos2α+sin2α+1 |
| cos2α |
| A、4 | ||
| B、6 | ||
| C、12 | ||
D、
|
考点：二倍角的余弦,同角三角函数基本关系的运用
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系，求得要求式子的值．
解答：
解：
=
=
=
=4，
故选：A．
| cos2α+sin2α+1 |
| cos2α |
| 2cos2α+2sinαcosα |
| cos2α-sin2α |
| 2+2tanα |
| 1-tan2α |
| 2+1 | ||
1-
|
故选：A．
点评：本题主要考查同角三角函数的基本关系的应用，属于基础题．
练习册系列答案
相关题目
一个扇形OAB的面积是1cm2，它的周长是4cm，则弦|AB|=（ ）
| A、sin1 | B、cos1 |
| C、2sin1 | D、sin2 |
不等式
＜
的解集是（ ）
| 1 |
| x |
| 1 |
| 2 |
| A、{x|x＜2} |
| B、{x|x＞2} |
| C、{x|0＜x＜2} |
| D、{x|x＜0或x＞2} |
已知抛物线y=ax2经过点（1，-
），则该抛物线的焦点坐标为（ ）
| 1 |
| 4 |
A、（0，-
| ||
B、（0，-
| ||
| C、（0，-1） | ||
| D、（0，1） |
如图，在△ABC中，∠BAC=90°，AD⊥BC，垂足为D，E是AC上的一点，若AF⊥BE，垂足为F，求证：∠BFD=∠C．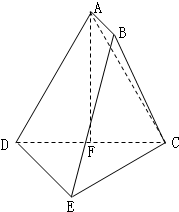
已知在多面体ABCDE中，AB⊥平面ACD，AB=1，DE∥AB，AC=AD=CD=DE=2，F为CD的中点．