题目内容
19. 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
分析 由三视图可知:该几何体是如图所示的三棱锥,其中侧面PAC⊥面ABC,△PAC是边长为2的正三角形,△ABC是边AC=2,边AC上的高OB=1,PO=$\sqrt{3}$为底面上的高.据此可计算出表面积和体积.
解答 解:由三视图可知:该几何体是如图所示的三棱锥,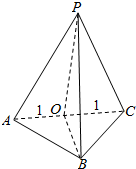
其中侧面PAC⊥面ABC,△PAC是边长为2的正三角形,△ABC是边AC=2,
边AC上的高OB=1,PO=$\sqrt{3}$为底面上的高.
于是此几何体的体积V=$\frac{1}{3}$S△ABC•PO=$\frac{1}{3}•$$\frac{1}{2}$×2×1×$\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
几何体的表面积S=S△PAC+S△ABC+2S△PAB=$\frac{1}{2}$×$\sqrt{3}$×2+$\frac{1}{2}$×2×1+2×$\frac{1}{2}$×$\sqrt{{1}^{2}+{1}^{2}}$×$\sqrt{{2}^{2}-(\frac{{1}^{2}+{1}^{2}}{2})^{2}}$=$\sqrt{3}$+1+$\sqrt{7}$.
故答案为:$\frac{\sqrt{3}}{3}$,$\sqrt{3}$+1+$\sqrt{7}$.
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
9.“?x∈R,x2-2>0”的否定是( )
| A. | ?x∈R,x2-2<0 | B. | ?x∈R,x2-2≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$-2<0 | D. | ?x0∈R,x${\;}_{0}^{2}$-2≤0 |
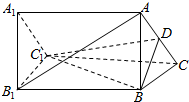 已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.
已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.