题目内容
11.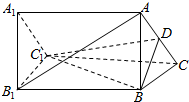 已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.
已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.(1)求证:AB1∥平面DBC1;
(2)若AB1⊥BC1,求以BC1为棱DBC1与CBC1为面的二面角的度数.
分析 (1)连结B1C,交BC1于点O,连结OD,由已知得OD∥AB1,由此能证明AB1∥平面DBC1.
(2)根据二面角的定义作出二面角的平面角,根据三角形的边角关系 进行求解即可.
解答 证明:(1)连结B1C,交BC1于点O,连结OD,
∵A1B1C1-ABC是正三棱柱,
∴BCC1B1是矩形,∴O是B1C的中点,
又D是AC的中点,∴OD∥AB1,
∵OD?平面DBC1,AB1?平面DBC1,
∴AB1∥平面DBC1.
(2)在平面ABC内,作DF⊥BC于F,则DF⊥面B1BCC1,
连接OF,则OF是OD在底面的射影,
∵AB1⊥BC1,∴由(1)知,AB1∥DE,
∴DE⊥BC1,
由三垂线逆定理得BC1⊥EF,
则∠DOF是以BC1为棱DBC1与CBC1为面的二面角的平面角,设为θ,
设AC=1,则CD=$\frac{1}{2}$,则DF=CD$•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,CF=$\frac{1}{4}$,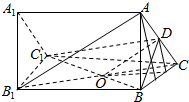
取BC的中点G,
∵OB=OC,∴GO⊥BC,
则GF=CF=$\frac{1}{4}$,OF=$\frac{\sqrt{3}}{4}$,
则tan∠DOF=$\frac{DF}{OF}$=1,
即∠DOF=45°.
即二面角的平面角为45°.
点评 本题主要考查线面平行的判定,以及二面角的求解,利用线面平行的判定定理以及二面角的定义作出二面角的平面角是解决本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
3.据统计,夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),则在此期间的某一天,该旅游景点的游客人数不超过1300的概率为( )
| A. | 0.4987 | B. | 0.8413 | C. | 0.9772 | D. | 0.9987 |
20.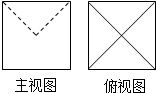 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )| A. | 24 | B. | 20+4$\sqrt{2}$ | C. | 24+4$\sqrt{2}$ | D. | 20+4$\sqrt{3}$ |
 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.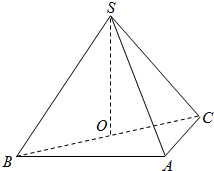 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.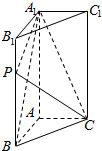 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).