题目内容
9．cos$\frac{2π}{3}$•tan$\frac{7π}{4}$的值为$\frac{1}{2}$．分析 利用诱导公式及特殊角的三角函数值即可计算求解．
解答 解：cos$\frac{2π}{3}$•tan$\frac{7π}{4}$
=cos（$π-\frac{π}{3}$）tan（2$π-\frac{π}{4}$）
=cos$\frac{π}{3}$tan$\frac{π}{4}$
=$\frac{1}{2}$×1
=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题主要考查 诱导公式及特殊角的三角函数值在三角函数化简求值中的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的体积是$\frac{\sqrt{3}}{3}$，表面积是$\sqrt{3}$+1+$\sqrt{7}$．
20．
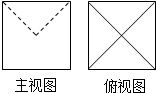某几何体正视图与侧视图相同，其正视图与俯视图如图所示，且图中的四边形都是边长为2的正方形，正视图中两条虚线互相垂直，则该几何体的表面积是（ ）
某几何体正视图与侧视图相同，其正视图与俯视图如图所示，且图中的四边形都是边长为2的正方形，正视图中两条虚线互相垂直，则该几何体的表面积是（ ）| A． | 24 | B． | 20+4$\sqrt{2}$ | C． | 24+4$\sqrt{2}$ | D． | 20+4$\sqrt{3}$ |
17．曲线y=f（x）在点（x0，f（x0）））处的切线的倾斜角是$\frac{π}{4}$，f′（x0）的值为（ ）
| A． | $\frac{π}{4}$ | B． | -$\frac{π}{4}$ | C． | -1 | D． | 1 |
14．已知椭圆的两个焦点分别为F1、F2，其中F1与抛物线x2=8y的焦点重合，过F1且不与x轴平行的直线与椭圆交于A、B两点，若△ABF2为等腰直角三角形，则e2=（ ）
| A． | 7-4$\sqrt{3}$ | B． | 5-2$\sqrt{6}$ | C． | 9-6$\sqrt{2}$ | D． | 8-2$\sqrt{15}$ |