题目内容
10.已知命题p:x≤1,命题q:$\frac{1}{x}$≥1,则命题p是命题q的必要不充分条件.分析 命题q:$\frac{1}{x}$≥1,即$\frac{x-1}{x}$≤0,等价于x(x-1)≤0,x≠0,解得0<x≤1.即可判断出结论.
解答 解:命题p:x≤1,命题q:$\frac{1}{x}$≥1,∴$\frac{x-1}{x}$≤0,等价于x(x-1)≤0,x≠0,解得0<x≤1.
则命题p是命题q的必要不充分条件.
故答案为:必要不充分.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.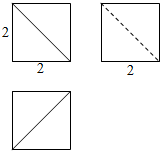 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{20}{3}$ | B. | 18 | C. | $24+2\sqrt{3}$ | D. | $18+2\sqrt{3}$ |
15.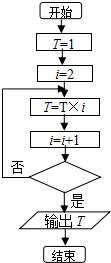 若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
 若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )| A. | i<5? | B. | i>5? | C. | i>6? | D. | i≥5? |
20.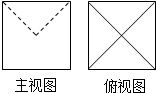 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的表面积是( )| A. | 24 | B. | 20+4$\sqrt{2}$ | C. | 24+4$\sqrt{2}$ | D. | 20+4$\sqrt{3}$ |
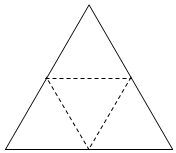 如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.
如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.
 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.