题目内容
7.设有5件产品,其中含有2件次品,从中任意抽取3件进行检查,(1)求取出的3件中恰有一个次品的概率;
(2)求抽得的产品中所含的次品数ξ的概率分布.
分析 (1)确定基本事件的个数,利用古典概型的概率公式,即可求取出的3件中恰有一个次品的概率;
(2)随机变量ξ的所有可能取值为0,1,2,求出相应的概率,即可求抽得的产品中所含的次品数ξ的概率分布.
解答 解:(1)设A表示事件“取出的3件中恰有一个次品”,…(1分)
P(A)=$\frac{C_2^1C_3^2}{C_5^3}=\frac{3}{5}$…(2分)
(2)随机变量ξ的所有可能取值为0,1,2,…(3分)
并且P(ξ=0)=$\frac{C_2^0C_3^3}{C_5^3}=\frac{1}{10}$,P(ξ=1)=$\frac{C_2^1C_3^2}{C_5^3}=\frac{3}{5}$,P(ξ=2)=$\frac{C_2^2C_3^1}{C_5^3}=\frac{3}{10}$…(6分)
所以ξ的概率分布为
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{3}{5}$ | $\frac{3}{10}$ |
点评 本题考查概率的计算,考查概率分布,正确求概率是关键.

练习册系列答案
相关题目
15.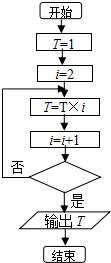 若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
 若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )| A. | i<5? | B. | i>5? | C. | i>6? | D. | i≥5? |
12.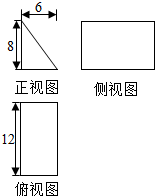 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )| A. | $\frac{32π}{3}$ | B. | 16π | C. | 32π | D. | $\frac{16π}{3}$ |
17.曲线y=f(x)在点(x0,f(x0)))处的切线的倾斜角是$\frac{π}{4}$,f′(x0)的值为( )
| A. | $\frac{π}{4}$ | B. | -$\frac{π}{4}$ | C. | -1 | D. | 1 |

 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.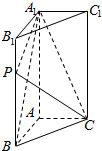 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AB=AC=1,AA1=2,点P是棱BB1上一点,满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$(0≤λ≤1).