��Ŀ����
12����֪����$\overrightarrow{a}$=��2��3����$\overrightarrow{b}$=��-1��2������|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{17}$����m$\overrightarrow{a}$+4$\overrightarrow{b}$��$\overrightarrow{a}$-2$\overrightarrow{b}$���ߣ���m��ֵΪ-2������ ����������ģ���������ߵ�������⼴�ɣ�
��� �⣺��$\overrightarrow{a}$=��2��3����$\overrightarrow{b}$=��-1��2����
��$\overrightarrow{a}-2\overrightarrow{b}$=��4��-1����
��|$\overrightarrow{a}-2\overrightarrow{b}|$=$\sqrt{17}$��
��m$\overrightarrow{a}+4\overrightarrow{b}$=��2m-4��3m+8����
��m$\overrightarrow{a}$+4$\overrightarrow{b}$����$\overrightarrow{a}$-2$\overrightarrow{b}$���ߣ�
��4����3m+8��-��-1��•��2m-4��=0��
��ã�m=-2��
���� ������Ҫ����������ģ�������Ĺ��ߣ����ڻ����⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
20��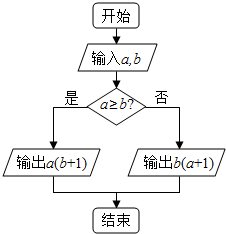 ����ʵ��a��b����������a*b������ԭ����ͼ��ʾ����ʽ�ӣ�$\frac{1}{2}$��-2*lne3��ֵΪ��������
����ʵ��a��b����������a*b������ԭ����ͼ��ʾ����ʽ�ӣ�$\frac{1}{2}$��-2*lne3��ֵΪ��������
 ����ʵ��a��b����������a*b������ԭ����ͼ��ʾ����ʽ�ӣ�$\frac{1}{2}$��-2*lne3��ֵΪ��������
����ʵ��a��b����������a*b������ԭ����ͼ��ʾ����ʽ�ӣ�$\frac{1}{2}$��-2*lne3��ֵΪ��������| A�� | 8 | B�� | 15 | C�� | 16 | D�� | $\frac{3}{2}$ |
1��ʹ����y=3-2cosxȡ����Сֵʱ��x�ļ���Ϊ��������
| A�� | {x|x=2k��+��k��Z} | B�� | {x|x=2k��k��Z} | C�� | $\{\left.x\right|x=2k��+\frac{��}{2}��k��Z\}$ | D�� | $\{\left.x\right|x=2k��-\frac{��}{2}��k��Z\}$ |
 ��ͼ����������PABC �У���PAB��PBC��PAC������ֱ��
��ͼ����������PABC �У���PAB��PBC��PAC������ֱ��