题目内容
14.已知P在△ABC所在平面内,$\overrightarrow{AP}$=λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$),λ∈[0,+∞),则点P的轨迹一定经过△ABC的垂心.分析 可先根据积为零得出$\overrightarrow{BC}$与$λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC})$垂直,可得点P在BC的高线上,从而得到结论.
解答 解:∵$\overrightarrow{OP}=\overrightarrow{OA}$+λ$(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC})$,
∴$\overrightarrow{AP}$=λ($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$),
又$\overrightarrow{BC}•(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC})$=-$|\overrightarrow{BC}|+|\overrightarrow{BC}|$=$\overrightarrow{0}$,
∴$\overrightarrow{BC}$与$λ(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC})$垂直,
即$\overrightarrow{AP}⊥\overrightarrow{BC}$,
∴点P在BC的高线上,即P的轨迹过△ABC的垂心,
故答案为:垂心.
点评 本题主要考查了向量在几何中的应用、空间向量的加减法、轨迹方程、以及三角形的五心等知识,属于中档题

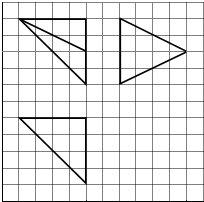 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )