题目内容
13．教室内有一根直尺，无论怎样放置，在地面上总有这样的直线，它与直尺所在直线（ ）| A． | 垂直 | B． | 异面 | C． | 平行 | D． | 相交 |
分析 由题意得可以分两种情况讨论：①当直尺所在直线与地面垂直时；②当直尺所在直线若与地面不垂直时，再分别借助于线面垂直的性质定理与三垂线定理得到答案
解答 解：由题意得可以分两种情况讨论：
①当直尺所在直线与地面垂直时，则地面上的所有直线都与直尺垂直，则底面上存在直线与直尺所在直线垂直；
②当直尺所在直线若与地面不垂直时，则直尺所在的直线必在地面上有一条投影线，在平面中一定存在与此投影线垂直的直线，由三垂线定理知，与投影垂直的直线一定与此斜线垂直，则得到地面上总有直线与直尺所在的直线垂直．
∴教室内有一直尺，无论怎样放置，在地面总有这样的直线与直尺所在直线垂直．
故选A
点评 本题只要考查空间中直线与平面之间的位置关系，以及考查空间中直线与直线的位置关系，解决此类问题关键是熟练掌握线面垂直的性质定理与三垂线定理
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
3．在△ABC中，$\overrightarrow{AD}$=$2\overrightarrow{DB}$，若$\overrightarrow{CB}$=$\overrightarrow{a}$，$\overrightarrow{CA}$=$\overrightarrow{b}$，则$\overrightarrow{CD}$=（ ）
| A． | $\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$ | B． | $\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$ | C． | $\frac{3}{5}\overrightarrow{a}+\frac{4}{5}\overrightarrow{b}$ | D． | $\frac{4}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$ |
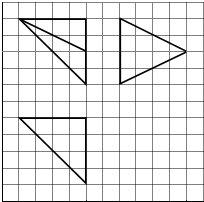如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各个面中，直角三角形的个数是（ ）