设$0＜θ＜\frac{π}{2}$.向量$\overrightarrow a=$.$\overrightarrow b=$.若$\vec a$⊥$\vec b$.则tanθ=$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

11．设$0＜θ＜\frac{π}{2}$，向量$\overrightarrow a=（sin2θ，cosθ）$，$\overrightarrow b=（1，-cosθ）$，若$\vec a$⊥$\vec b$，则tanθ=$\frac{1}{2}$．

分析根据向量的数量积的定义结合两向量垂直的数量积表示求解即可．

解答解：向量$\overrightarrow{a}$=（sin2θ，cosθ），$\overrightarrow{b}$=（1，-cosθ），$\overrightarrow{a}⊥\overrightarrow{b}$，
∴sin2θ-cos²θ=0
又0＜θ$＜\frac{π}{2}$，
tanθ=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$

点评本题主要考查向量的数量积以及向量的垂直，属于基础题．

练习册系列答案

2．以A（4，5）为顶点，试在x轴上找一点B，在直线2x-y+2=0上找一点C，使得△ABC周长最小．

19．已知集合M是同时满足下列两个性质的函数f（x）的全体
①函数f（x）在其定义域上是单调函数；②f（x）的定义域内存在区间[a，b]，使得f（x）在[a，b]上的值域为[$\frac{a}{2}，\frac{b}{2}$]．
（1）判断g（x）=x³是否属于M，若是，求出所有满足②的区间[a，b]，若不是，说明理由；
（2）若$h（x）=\sqrt{x-1}+t∈M$，求实数t的取值范围．

6．若关于x的不等式x²-4x≥m对任意x∈（0，1]恒成立，则m的取值范围是（-∞，-3]．

16．两条平行线3x+4y-12=0与ax+8y-4=0之间的距离为（　　）

3．设集合P={x|$\int_0^x{（{3{t^2}-10t+6}）}dt$=0}，则集合P的所有子集个数是（　　）

20．

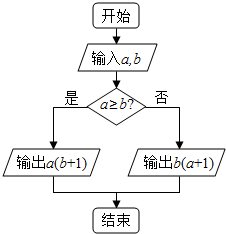对于实数a和b，定义运算a*b，运算原理如图所示，则式子（$\frac{1}{2}$）^-2*lne³的值为（　　）

1．使函数y=3-2cosx取得最小值时的x的集合为（　　）

$\{\left.x\right|x=2kπ+\frac{π}{2}，k∈Z\}$

D．

$\{\left.x\right|x=2kπ-\frac{π}{2}，k∈Z\}$

试题分类