题目内容
已知F1、F2分别为椭圆C：
+
=1（a＞b＞0）的左、右焦点，P（
，t）为椭圆C上第一象限的点，过点P作两互相垂直的直线L1、L2，L1经过椭圆C左顶点A，L2经过右焦点F2．
（1）求椭圆离心率；
（2）将直线L1绕点P逆时针旋转30°后，直线L1通过左焦点F1，且与椭圆交于B点，此时△PF2B的面积为
，求椭圆C的方程．
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 4 |
（1）求椭圆离心率；
（2）将直线L1绕点P逆时针旋转30°后，直线L1通过左焦点F1，且与椭圆交于B点，此时△PF2B的面积为
35
| ||
| 11 |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）利用
•
=0，可得t2=
c-
，根据P在椭圆上可得
+
=1，由此可求椭圆离心率；
（2）利用tan30°=tan（β-α）=
，F1P：y=
（x+c），
+
=1，△PF2B的面积为
，即可求椭圆C的方程．
| AP |
| F2P |
| 5a |
| 4 |
| 5a2 |
| 16 |
| 1 |
| 16 |
| t2 |
| b2 |
（2）利用tan30°=tan（β-α）=
| ||
| 3 |
| 4t |
| a+4c |
| x02 |
| a2 |
| y02 |
| b2 |
35
| ||
| 11 |
解答：
解：（1）由题意得：A（-a，0）、P（
，t）、F1（-c，0）、F2（c，0）
∴
=（
，t）、
=（
-c，t），
∴
•
=
-
c+t2=0，
∴t2=
c-
①
∵P在椭圆上
∴
+
=1 ②
联合①②得
15（a2-c2）=20ac-5a2，
整理得（3e-2）（e+2）=0
∴e=
或e=-2舍
（2）过点P作PH⊥x轴，垂足为H
tanα=tan∠HPF1=
，tanβ=tan∠APH=
tan30°=tan（β-α）=
③
设B（x0，y0），则kF1P=
F1P：y=
（x+c） ④
∵B在椭圆上
∴
+
=1 ⑤
∵△PF2B的面积为
，
∴S=
•2c•t+
•2c•y0=
，⑥
联合③④⑤⑥得a2=9，c2=4
∴椭圆C的方程为
+
=1．
| a |
| 4 |
∴
| AP |
| 5a |
| 4 |
| F2P |
| a |
| 4 |
∴
| AP |
| F2P |
| 5a2 |
| 16 |
| 5a |
| 4 |
∴t2=
| 5a |
| 4 |
| 5a2 |
| 16 |
∵P在椭圆上
∴
| 1 |
| 16 |
| t2 |
| b2 |
联合①②得
15（a2-c2）=20ac-5a2，
整理得（3e-2）（e+2）=0
∴e=
| 2 |
| 3 |
（2）过点P作PH⊥x轴，垂足为H
tanα=tan∠HPF1=
c+
| ||
| t |
a+
| ||
| t |
tan30°=tan（β-α）=
| ||
| 3 |
设B（x0，y0），则kF1P=
| 4t |
| a+4c |
F1P：y=
| 4t |
| a+4c |
∵B在椭圆上
∴
| x02 |
| a2 |
| y02 |
| b2 |
∵△PF2B的面积为
35
| ||
| 11 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
35
| ||
| 11 |
联合③④⑤⑥得a2=9，c2=4
∴椭圆C的方程为
| x2 |
| 9 |
| y2 |
| 5 |
点评：本题考查椭圆的方程与性质，考查三角形面积的计算，考查向量知识的运用，考查学生分析解决问题的能力，难度大．
练习册系列答案
阅读快车系列答案
相关题目
已知变量x、y满足条件
，则2x+y的最大值是（ ）
|
| A、3 | B、6 | C、9 | D、12 |
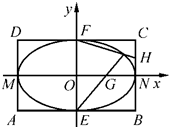如图，矩形ABCD中，|AB|=4，|BC|=2，E，F，M，N分别是矩形四条边的中点，G，H分别是线段ON，CN的中点．
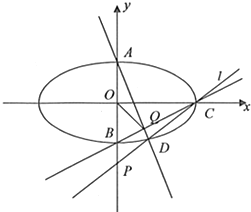如图，已知连接椭圆