题目内容
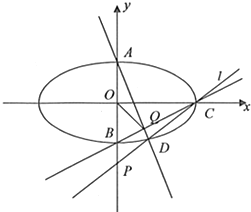 如图,已知连接椭圆
如图,已知连接椭圆| x2 |
| a2 |
| 2 |
(1)求a的值;
(2)判断
| OP |
| OQ |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出4×
×a×1=2
,由此能求出a=
.
(2)椭圆方程为
+y2=1,其右顶点为C(
,0),设直线CD:y=k(x-
),联立直线CD和椭圆的方程,得:(1+2k2)x2-4
k2x+4k2-2=0,由此能推导出
•
为定值1.
| 1 |
| 2 |
| 2 |
| 2 |
(2)椭圆方程为
| x2 |
| 2 |
| 2 |
| 2 |
| 2 |
| OP |
| OQ |
解答:
解:(1)∵连接椭圆
+y2=1(a>1)的四个顶点得到的菱形的面积为2
,
∴4×
×a×1=2
,
解得a=
.
(2)
•
为定值,证明如下:
由(1)知椭圆方程为
+y2=1,
其右顶点为C(
,0),
设直线CD:y=k(x-
),k≠0,
则点P的坐标为(0,-
k),
联立直线CD和椭圆的方程,得:(1+2k2)x2-4
k2x+4k2-2=0,
由韦达定理,得xC•xD=
,
∴xD=
,
设点Q的坐标为(x′,y′),直线BC的方程为:y=
(x-
),
A、Q、D三点共线,
则
,
∴
=
=
=
,
解得y′=-
,
则
•
=(0,-
k)•(x′,-
)=1,
∴
•
为定值1.
| x2 |
| a2 |
| 2 |
∴4×
| 1 |
| 2 |
| 2 |
解得a=
| 2 |
(2)
| OP |
| OQ |
由(1)知椭圆方程为
| x2 |
| 2 |
其右顶点为C(
| 2 |
设直线CD:y=k(x-
| 2 |
则点P的坐标为(0,-
| 2 |
联立直线CD和椭圆的方程,得:(1+2k2)x2-4
| 2 |
由韦达定理,得xC•xD=
| 4k2-2 |
| 1+2k2 |
∴xD=
2
| ||||
| 1+2k2 |
设点Q的坐标为(x′,y′),直线BC的方程为:y=
| 1 | ||
|
| 2 |
A、Q、D三点共线,
则
|
∴
| y′-1 |
| y′+1 |
| ||
| x0 |
| ||||
| x0 |
| ||
1-
|
解得y′=-
| 1 | ||
|
则
| OP |
| OQ |
| 2 |
| 1 | ||
|
∴
| OP |
| OQ |
点评:本题考查椭圆中参数的求法,考查向量的数量积是否为定值的判断与求法,解题时要认真审题,注意韦达定理的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
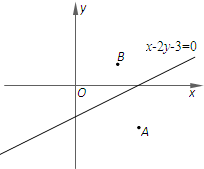 已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.
已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.